Học có giám sát (Supervised Learning) là mô hình dữ liệu được huấn luyện trên một tập dữ liệu đã được gán nhãn; tùy vào đặc tính của tập dữ liệu mà chúng ta có thể sử dụng các mô hình phân loại và hồi quy khác nhau: Mô hình Cây quyết định (Decision Trees), mô hình Random Forest, Mô hình Bayes (Naive Bayes Classifiers), Mô hình KNN (K-NN Classifiers) và mô hình SVM (Support Vector Machines), hồi quy đơn biến, hồi quy đa biến, hồi quy logistic.
Học có giám sát bằng mô hình K-Nearest Neighbors
Mô hình K-Nearest Neighbors thuộc nhóm mô hình phi tham số (non-parametric), nghĩa là mô hình không xây dựng dựa trên một hàm số cụ thể trong giai đoạn huấn luyện, mà thực hiện tính toán trực tiếp khi dự đoán dựa trên giả định rằng các điểm dữ liệu tương tự thường nằm gần nhau trong không gian thuộc tính. Mô hình K-Nearest Neighbors được sử dụng chủ yếu để phân loại.
Nguyên lý hoạt động của mô hình K-Nearest Neighbors
Khi có một điểm dữ liệu mới cần dự đoán, mô hình K-Nearest Neighbors sẽ đi tìm k điểm dữ liệu gần nhất trong tập huấn luyện (ở đây, k được gọi là số lượng lân cận gần nhất). Khoảng cách giữa điểm mới và các điểm trong tập huấn luyện được tính toán bằng các khoảng cách như Euclidean, Manhattan, Minkowski, Mahalanobis, … Trong đó, khoảng cách Euclidean được sử dụng phổ biến nhất.
Khoảng cách Euclidean giữa hai điểm x và y trong không gian n chiều là:
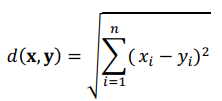
Khoảng cách Manhattan giữa hai điểm x và y trong không gian n chiều là:
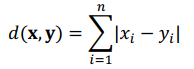
Khoảng cách Minkowski giữa hai điểm x và y trong không gian n chiều với trọng số p≥1 là:
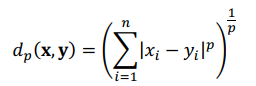
Sau khi xác định được k điểm gần nhất, mô hình K-Nearest Neighbors sẽ dựa vào nhãn của các điểm này để đưa ra dự đoán:
- Phân loại: mô hình K-Nearest Neighbors sử dụng nguyên tắc biểu quyết đa số (majority voting), tức là nhãn xuất hiện nhiều nhất trong k lân cận sẽ được gán cho điểm mới. Ví dụ, nếu trong 9 lân cận gần nhất có 5 điểm mang nhãn A và 4 điểm mang nhãn B thì điểm mới sẽ được gán nhãn A.
- Hồi quy: mô hình K-Nearest Neighbors sẽ dự đoán giá trị liên tục cho điểm mới bằng cách lấy trung bình hoặc trung bình có trọng số của giá trị các lân cận gần nhất.
Các bước được thực hiện trong mô hình K-Nearest Neighbors
- Chọn giá trị k: Đây là số lượng lân cận gần nhất được xét để dự đoán. Giá trị k ảnh hưởng lớn đến kết quả, k quá nhỏ có thể gây nhiễu, k quá lớn có thể làm mất tính đặc trưng.
- Tính khoảng cách: Tính khoảng cách giữa điểm dữ liệu mới và tất cả điểm trong tập huấn luyện.
- Chọn k lân cận gần nhất: Lấy ra k điểm có khoảng cách nhỏ nhất.
- Dự đoán nhãn hoặc giá trị: Dựa vào nhãn của k lân cận để phân loại hoặc lấy trung bình giá trị để hồi quy.
Ứng dụng của mô hình K-Nearest Neighbors
Mô hình K-Nearest Neighbors được ứng dụng trong:
- Phân loại văn bản, nhận dạng chữ viết, nhận dạng khuôn mặt.
- Hệ thống gợi ý.
- Phân loại hình ảnh.
- Chẩn đoán bệnh dựa trên triệu chứng.
- Dự báo tài chính, phân tích review.
Ưu điểm và nhược điểm của mô hình K-Nearest Neighbors
Ưu điểm của mô hình K-Nearest Neighbors
- Đơn giản, dễ hiểu và triển khai.
- Không cần huấn luyện và phù hợp với dữ liệu thay đổi liên tục.
- Không cần giả định phân phối dữ liệu.
- Thích ứng nhanh với dữ liệu mới mà không cần huấn luyện lại toàn bộ mô hình.
Nhược điểm của mô hình K-Nearest Neighbors
- Tính toán khoảng cách với toàn bộ dữ liệu huấn luyện khi dự đoán nên tốn thời gian và bộ nhớ khi tập dữ liệu lớn.
- Hiệu quả phụ thuộc vào việc chọn giá trị k và cách tính khoảng cách phù hợp.
- Hiệu suất giảm khi số chiều dữ liệu lớn.
Ví dụ học có giám sát bằng mô hình K-Nearest Neighbors trong R
Xét tập dữ liệu Iris.
Mục tiêu: Phân loại các loại hoa.
Quá trình được thực hiện tuần tự qua các bước sau đây:
Bước 1: Chuẩn bị dữ liệu;
Bước 2: Tiền xử lý và trực quan hóa dữ liệu;
Bước 3: Chuẩn hóa và chia dữ liệu;
Bước 4: Huấn luyện mô hình K-Nearest Neighbors và đánh giá kết quả;
Bước 5: Đánh giá mô hình;
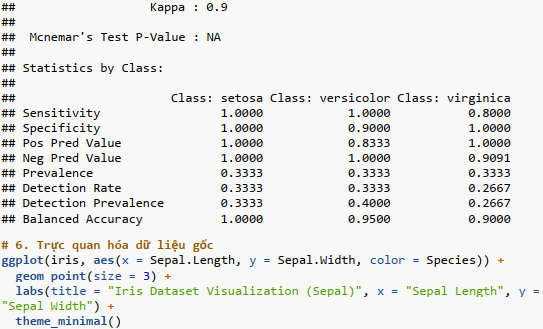
Bước 6: Trực quan hóa dữ liệu gốc;
Bước 7: Trực quan hóa kết quả dự đoán bằng mô hình K-Nearest Neighbors.


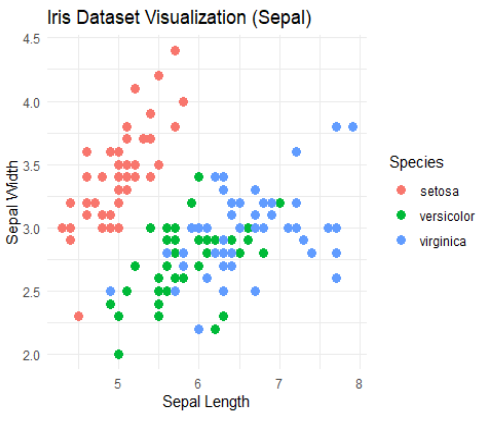

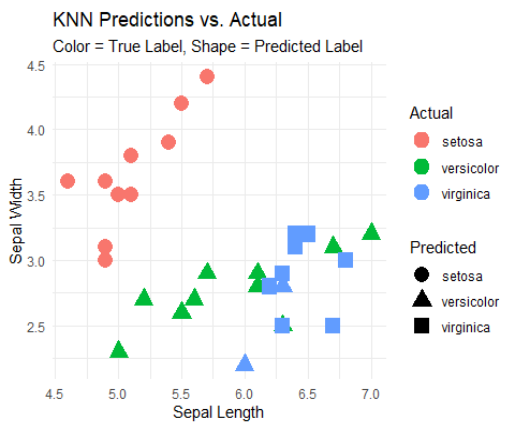
Kết Luận
Mô hình K-Nearest Neighbors là một mô hình học có giám sát mạnh mẽ, dễ hiểu nhưng đòi hỏi tối ưu hóa tham số và xử lý dữ liệu cẩn thận như chuẩn hoá và giảm chiều dữ liệu, chọn tham số k phù hợp và chọn cách tính khoản cách phù hợp để giảm thời gian tính toán. Mô hình K-Nearest Neighbors rất phù hợp với các bài toán có dữ liệu ít nhiễu và số chiều vừa phải.
Nhất Luận
----------------------------------------
Tài liệu tham khảo:
[1] R for Data Science. https://r4ds.had.co.nz/
[2] R for Data Science (2e). https://r4ds.hadley.nz/
[3] R for Data Science. https://bookdown.org/swen/R_for_Data_Science/
[4] R Packages (2e). https://r-pkgs.org/
[5] Advanced R. https://adv-r.hadley.nz/index.html#license
[6] Advanced R Solutions. https://advanced-r-solutions.rbind.io/
[7] Machine Learning with R. https://tuanvanle.wordpress.com/2017/04/19/machine-learning-with-r/
[8] Iris Species. https://www.kaggle.com/datasets/uciml/iris
