Trong các mô hình thống kê, người ta thường giả định phương sai không đổi (hay còn gọi là phương sai đồng nhất) để đảm bảo các tham số mô hình được ước tính một cách hiệu quả; giới hạn dự đoán và so sánh giữa các nhóm trường hợp khác nhau được tính toán đúng cách. Tuy nhiên trong thực tế, phương sai sai số tăng khi đáp ứng trung bình tăng, nếu tuân theo luật phân phối Poisson thì phương sai sẽ tỷ lệ thuận với giá trị trung bình.
Trong phần mềm Statgraphics Centurion, các quy trình như hồi quy Poisson được thiết kế để xử lý phương sai không cố định. Đối với những loại dữ liệu khác, cách thức thay đổi phương sai sẽ được xác định thông qua phân tích dữ liệu thực tế.
Ví dụ: Nghiên cứu trên 54 phụ nữ từ 20 đến 60 tuổi, với mục tiêu xác định mối quan hệ giữa huyết áp và tuổi tác, có bảng số liệu như Hình 1.
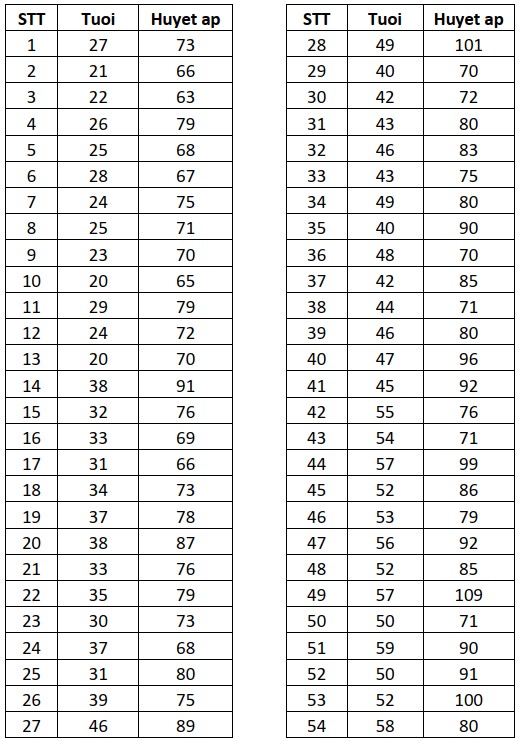
Hình 1: Bảng dữ liệu thu được từ nghiên cứu
Bước 1: Vẽ biểu đồ dữ liệu
Dữ liệu trong ví dụ này liên quan đến hai biến định lượng, để hiển thị mối quan hệ giữa chúng, sử dụng biểu đồ phân tán XY (Scatterplot).
Chọn X-Y Scatterplot => xuất hiện hộp thoại
Hình 2: Hộp thoại nhập dữ liệu cho biểu đồ phân tán XY
Biểu đồ kết quả hiển thị 54 quan sát:
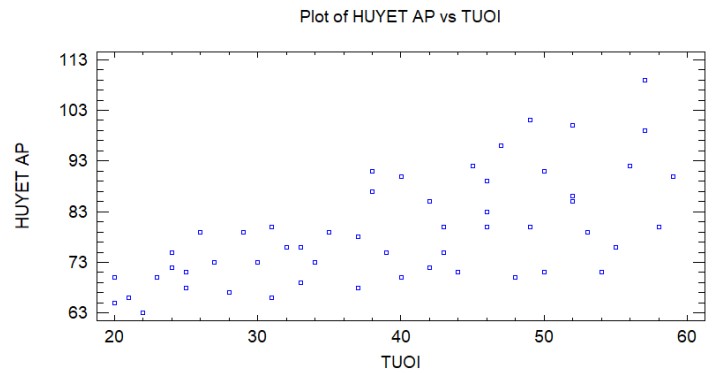
Hình 3: Biểu đồ phân tán XY cho 54 phụ nữ
Biểu đồ cho thấy, sự biến đổi của huyết áp có xu hướng tăng đáng kể khi tuổi tác tăng lên, đồng thời sai số cũng tăng lên cho thấy mô hình ban đầu có hiện tượng phương sai sai số thay đổi.
Bước 2: Điều chỉnh mô hình tuyến tính cho dữ liệu
Mô hình tuyến tính của mối quan hệ trong Hình 3 có dạng: Y = a + bX + ε
Trong đó, Y = huyết áp; X = tuổi; ε = Sai số ngẫu nhiên (Sai số ngẫu nhiên thường được coi là tuân theo phân phối chuẩn - Gaussian với giá trị trung bình bằng 0 và phương sai bằng σ2. Trong trường hợp này, độ lệch chuẩn của sai số (σ) dường như là một hàm của X).
Để khớp một đường thẳng với dữ liệu này bằng phương pháp bình phương tối thiểu thông thường, Statgraphics Centurion cung cấp quy trình hồi quy đơn giản.
Chọn: Relate – One Factor – Simple Regression
Kết quả hiện thị:
Hình 4: Hộp thoại nhập dữ liệu cho mô hình hồi quy đơn giản
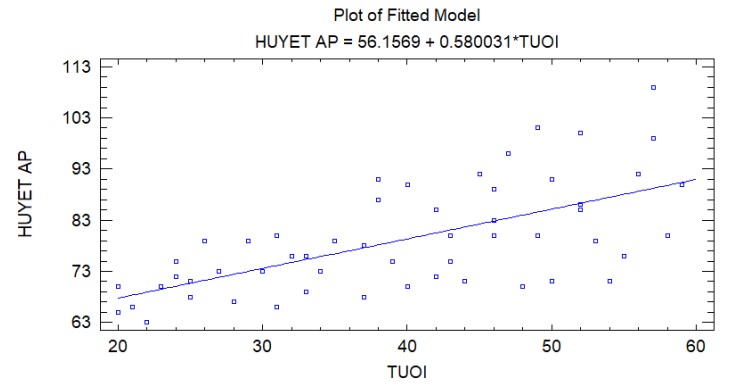
Hình 5: Mô hình tuyến tính được trang bị sử dụng bình phương tối thiểu
Hồi quy đơn giản tạo ra mô hình là ![]() bằng cách sử dụng bình phương tối thiểu thông thường, tìm đường thẳng chứa tổng bình phương còn lại:
bằng cách sử dụng bình phương tối thiểu thông thường, tìm đường thẳng chứa tổng bình phương còn lại:
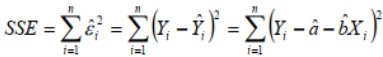
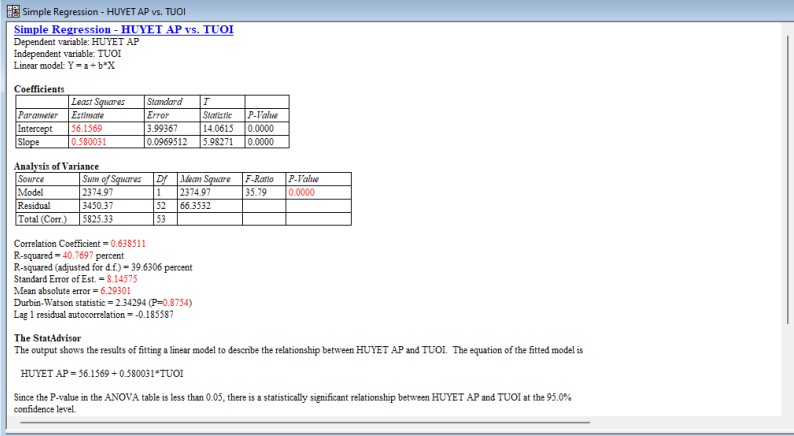
Hình 6: Tóm tắt phân tích hồi quy đơn giản
Các hệ số mô hình ước lượng và sai số chuẩn là: Intercept: 56.1569 ± 3.99367; Slope: 0.580031 ± 0.0969512.
Thống kê R bình phương, đo lường tỷ lệ biến thiên của huyết áp đã được mô hình giải thích là khoảng 40,8%. Khi khớp một đường thẳng với dữ liệu này, việc giảm trọng số cho các phần dư có độ lớn xác định đối với những giá trị của X có phương sai sai số lớn sẽ mang lại kết quả tốt hơn.
| Có hai cách chính điều chỉnh mô hình: (1) Biến đổi ổn định phương sai cho Y: căn bậc hai, logarit hoặc nghịch đảo biến thành một thước đo, sau đó bình phương tối thiểu số liệu được chuyển đổi; (2) Bình phương tối thiểu có trọng số: phần dư được tính trọng số nghịch đảo với phương sai và ước tính điểm chặn. |
Bước 3: Kiểm tra phương sai lỗi
Vẽ biểu đồ phần dư, nút đồ thị ![]() chọn Residuals versus X
chọn Residuals versus X
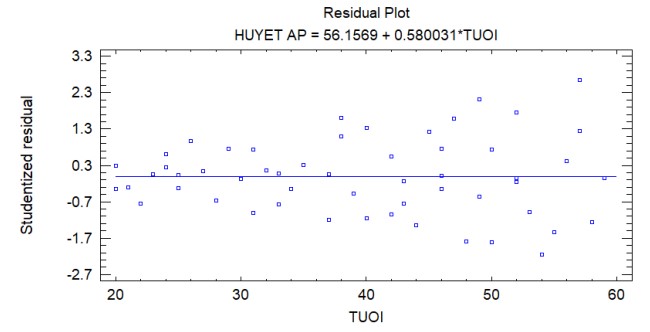
Hình 7: Đồ thị giá trị dư theo tuổi
Hình dạng phễu lớn, biểu thị phương sai sai số tăng khi độ tuổi tăng. Để mô hình hóa phương sai, tiến hành lưu kết quả, chia dữ liệu thành nhiều nhóm theo giá trị tuổi và ước tính độ lệch chuẩn trong mỗi nhóm. Chọn: Describe – Numeric Data – Subset Analysis.
Xuất hiện hộp thoại:
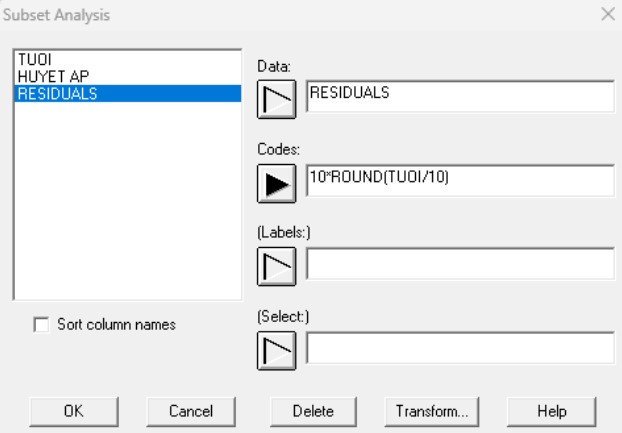
Hình 8: Hộp thoại nhập dữ liệu để phân tích tập hợp con
Trong đó, mã nhóm phần dư được sử dụng để làm tròn giá trị của tuổi về bội số gần nhất của 10. Kết quả hiển thị:
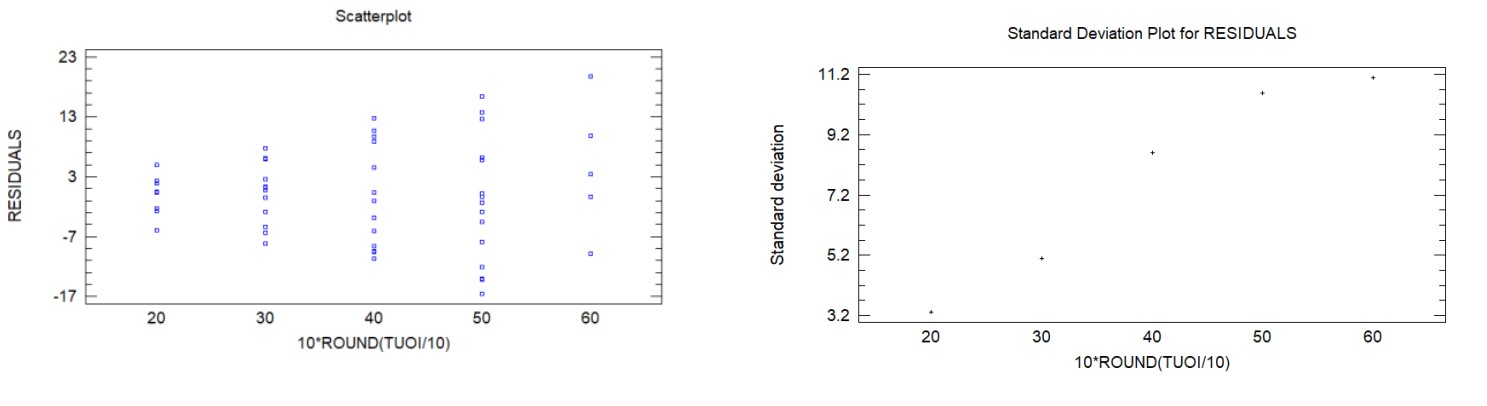
Hình 9: Biểu đồ phân tán phần dư được làm tròn thành các nhóm
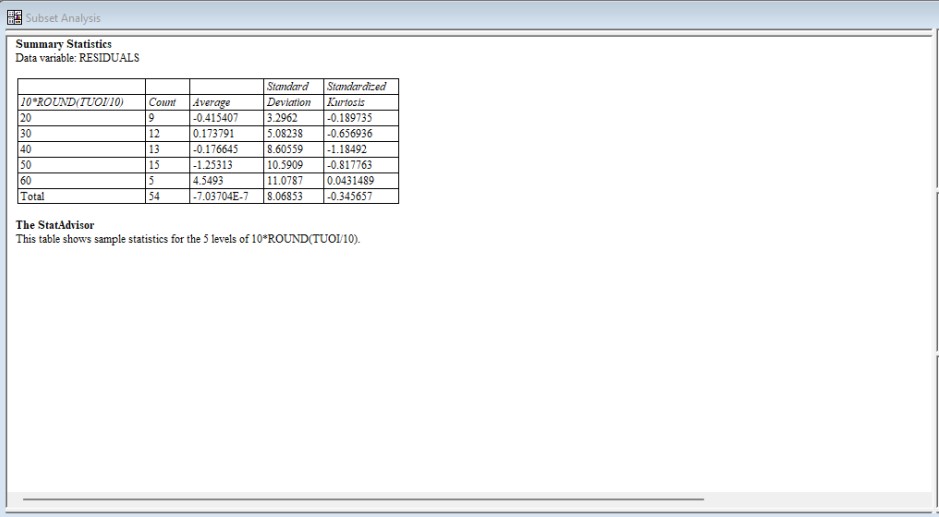
Hình 10: Bảng độ lệch chuẩn dư lượng theo độ tuổi
Mối quan hệ này gần như tuyến tính, cho thấy độ lệch chuẩn của sai số tăng tỷ lệ thuận với giá trị tuổi.
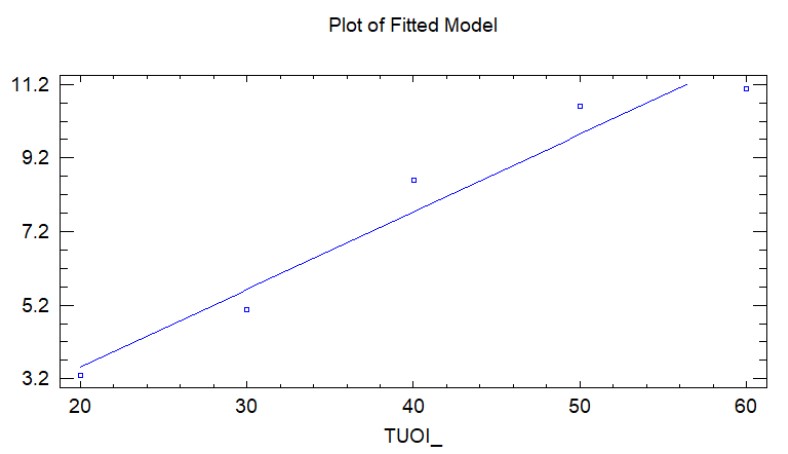
Hình 11: Đồ thị độ lệch chuẩn dư với mô hình cho Sigma
Một mô hình phù hợp cho dữ liệu này là độ lệch chuẩn của sai số tỷ lệ thuận với tuổi.
Bước 4: Áp dụng biến đổi ổn định phương sai
Khi phương sai của biến phản ứng tăng khi giá trị trung bình tăng, có thể ổn định phương sai bằng cách áp dụng phép biến đổi cho Y. Một số tình huống phổ biến:

Hình 12: Bảng các phép biến đổi ổn định phương sai
Hồi quy phi tuyến tính để điều chỉnh mô hình sử dụng bình phương tối thiểu phi tuyến tính trong Statgraphics Centurion: Chọn Relate – Multiple Factors – Nonlinear Regression.
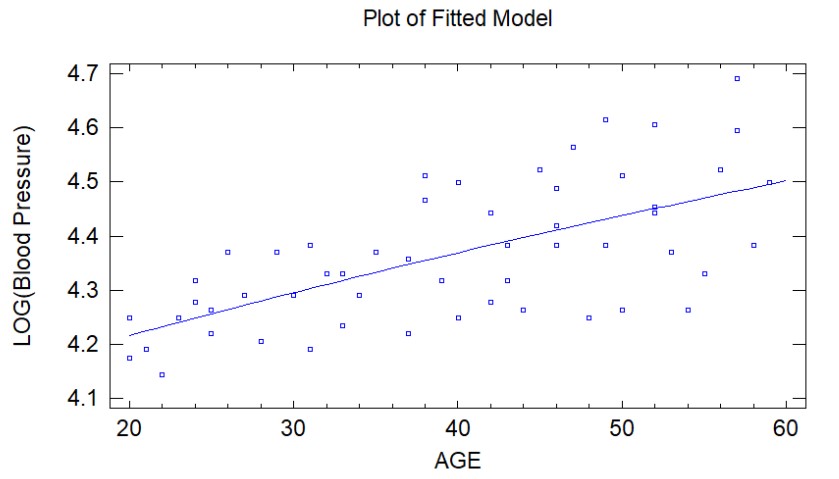
Hình 13: Mô hình hồi quy phi tuyến tính
Các hệ số ước tính được hiển thị trong bảng tóm tắt phân tích:
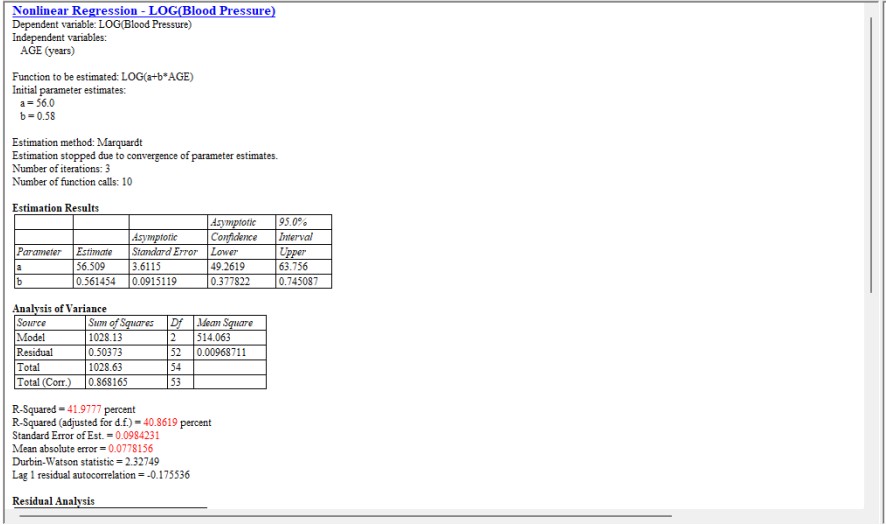
Hình 14: Tóm tắt phân tích cho mô hình hồi quy phi tuyến tính
So sánh các hệ số ước tính giữa hồi quy tuyến tính và phi tuyến:
| Hồi quy đơn giản sử dụng bình phương tối thiểu thông thường | Hồi quy phi tuyến tính với phép biến đổi ổn định phương sai | |
| Intercept | 56.1569 ± 3.99367 | 56.509 ± 3.6115 |
| Slope | 0.580031 ± 0.0969512 | 0.561454 ± 0.0915119 |
Hình 15: So sánh các hệ số mô hình
Hồi quy phi tuyến tính đã tạo ra một mô hình có độ dốc ít hơn mô hình ban đầu, sai số chuẩn của các hệ số cũng nhỏ hơn.
Bên cạnh việc sử dụng phép biến đổi ổn định phương sai, có thể cân nhắc áp dụng thêm phương pháp bình phương tối thiểu có trọng số.
Bước 5: Sử dụng bình phương tối thiểu có trọng số
Bằng cách sử dụng các trọng số wi tỷ lệ với phương sai sai số, tác động của phương sai thay đổi có thể giảm nhẹ. Một số trường hợp thường gặp là:

Hình 16: Bảng bình phương tối thiểu có trọng số
Hồi quy bội để điều chỉnh mô hình hồi quy bằng cách sử dụng bình phương tối thiểu có trọng số trong Statgraphics Centurion: Chọn Relate – Multiple Factors – Multiple Regression.
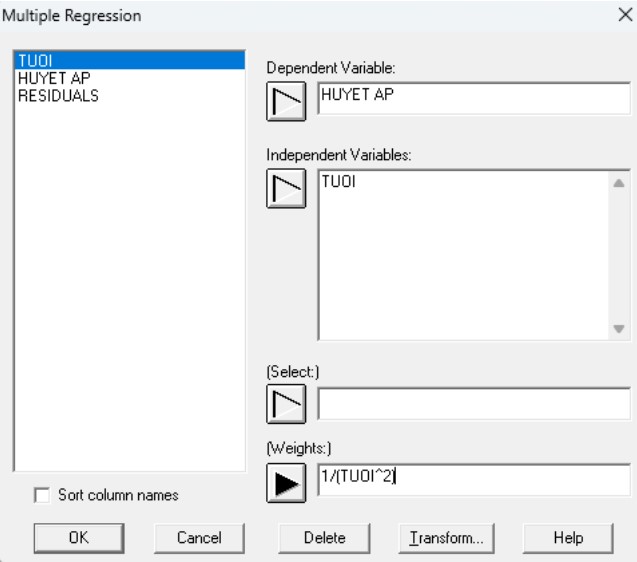
Hình 17: Hộp thoại nhập dữ liệu cho bình phương tối thiểu có trọng số
<
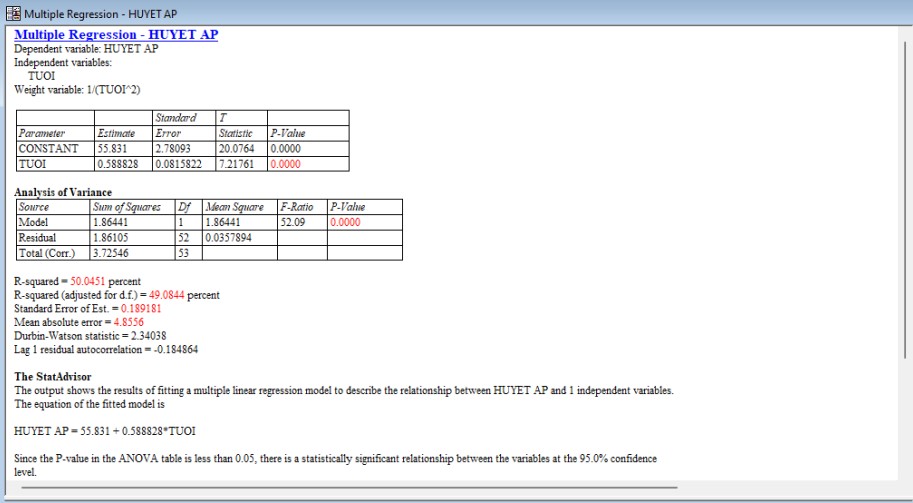
Hình 18: Tóm tắt phân tích cho bình phương tối thiểu có trọng số
Tóm tắt cả ba mô hình:
| Hồi quy đơn giản sử dụng bình phương tối thiểu thông thường | Hồi quy phi tuyến tính với phép biến đổi ổn định phương sai | Hồi quy bội sử dụng bình phương tối thiểu có trọng số | |
| Intercept | 56.1569 ± 3.99367 | 56.509 ± 3.6115 | 55.831 ± 2.78093 |
| Slope | 0.580031 ± 0.0969512 | 0.561454 ± 0.0915119 | 0.588828 ± 0.0815822 |
Hình 19: So sánh các hệ số mô hình
Có thể thấy, việc điều chỉnh mô hình nhằm ổn định phương sai đã mang lại những cải thiện rõ rệt trong quá trình phân tích dữ liệu. Sai số chuẩn của các hệ số được giảm đáng kể, góp phần nâng cao độ tin cậy của kết quả ước lượng. Mặc dù sự khác biệt giữa ba mô hình không quá lớn, nhưng nhờ vào việc ổn định phương sai, các giá trị dữ liệu đã được xử lý một cách nhất quán hơn, giảm thiểu sai lệch và tăng cường tính chính xác. Điều này cho thấy tầm quan trọng của việc kiểm soát phương sai trong quá trình xây dựng và phân tích mô hình, đặc biệt khi làm việc với các bộ dữ liệu có độ biến động cao.
Vân Anh
----------------------------------------
Tài liệu tham khảo chính
https://www.statgraphics.com/how-to-guides
---------------------------------------------------------------------------------------------------
