Trong các thí nghiệm nông nghiệp, nhất là các thí nghiệm ngoài ruộng đồng, bên cạnh các yếu tố thí nghiệm tác động trực tiếp đến kết quả nghiên cứu, đối tượng thí nghiệm còn chịu ảnh hưởng của các tác nhân bên ngoài khiến sai lệch kết quả. Do vậy, việc chọn cách bố trí thí nghiệm cho phù hợp là rất quan trọng.
Thí nghiệm trong nông nghiệp
Thí nghiệm là một phương pháp nghiên cứu khoa học, trong đó người ta tạo ra những hiện tượng, biến đổi nào đó trong điều kiện xác định để tìm hiểu, nghiên cứu, kiểm tra hoặc chứng minh bản chất, nguồn gốc của hiện tượng, biến đổi đó. Trong nông nghiệp, có nhiều cách phân loại thí nghiệm:
Theo điều kiện, tính chất thí nghiệm và quy mô
Thí nghiệm trong phòng: được thực hiện trong điều kiện nhân tạo. Con người kiểm soát các yếu tố tác động (nhiệt độ, độ ẩm, ánh sáng, các loại giá thể, dung dịch, môi trường,…). Vì vậy, ngoài yếu tố thí nghiệm, các tác nhân khác khó có thể ảnh hưởng, nên việc kết luận tác động của từng yếu tố và tương tác giữa các yếu tố thí nghiệm sẽ chính xác và ít sai số hơn. Đây cũng là luận cứ khoa học giải thích các hiện tượng tự nhiên. Tuy nhiên, trong thực tế, thí nghiệm trong phòng khó áp dụng ngay khi đưa vào sản xuất.
Thí nghiệm ngoài đồng: được tiến hành trong điều kiện tự nhiên trên đồng ruộng. Bên cạnh các yếu tố thí nghiệm, còn có những yếu tố khác của môi trường tác động đồng thời lên thí nghiệm (ví dụ: đất đai, khí hậu, côn trùng,…). Do vậy, kết quả thí nghiệm ngoài đồng ruộng mang tính thực tiễn cao, dễ chuyển giao trực tiếp vào sản xuất.
Theo mục đích nghiên cứu
Thí nghiệm một yếu tố: thí nghiệm với chỉ một yếu tố biến đổi, được nghiên cứu theo những mức độ khác nhau (ví dụ: các giống khác nhau, các liều lượng phân bón khác nhau, các loại chất điều hòa sinh trưởng khác nhau hay mật độ gieo trồng khác nhau,…).
Thí nghiệm nhiều yếu tố: thí nghiệm cho phép đánh giá tác động của từng yếu tố riêng lẻ và tương tác của các yếu tố đến đối tượng nghiên cứu (ví dụ: chế độ phân bón và mật độ gieo trồng cho các giống cây, nghiên cứu mức độ ánh sáng, nhiệt độ, pH và sự phối hợp giữa chúng).
Các kiểu bố trí thí nghiệm trong nông nghiệp
Tùy thuộc vào mục đích thí nghiệm và các điều kiện, quy mô thí nghiệm mà có những kiểu bố trí thí nghiệm phù hợp.
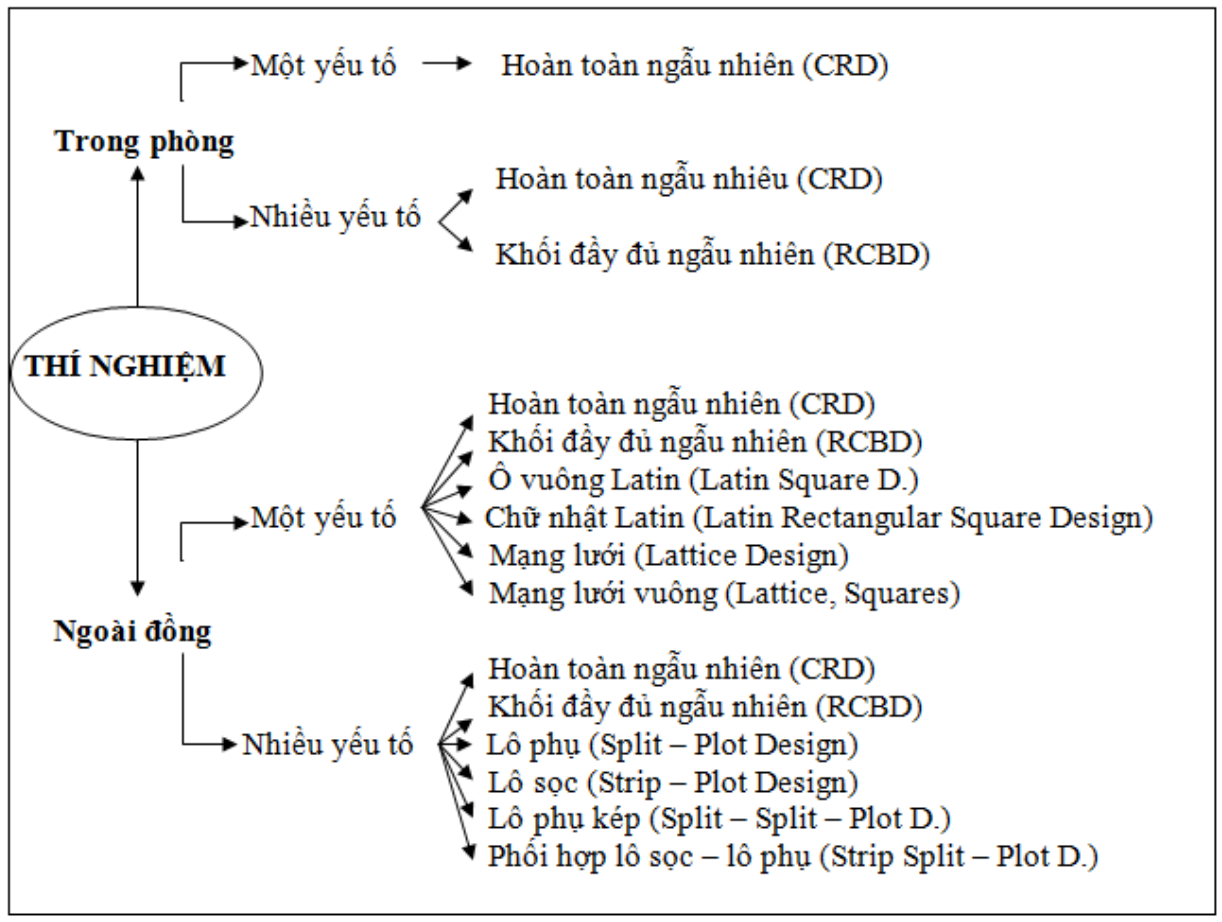
Hình 1. Các loại thí nghiệm và kiểu bố trí thí nghiệm trong nông nghiệp
Bố trí kiểu hoàn toàn ngẫu nhiên (CRD)
Các công thức thí nghiệm (nghiệm thức) được đặt vào các ô (hoặc các vị trí) hoàn toàn ngẫu nhiên, đảm bảo có cơ hội nhận điều kiện như nhau. Kiểu bố trí này chỉ phù hợp với các thí nghiệm hoàn toàn đồng nhất như trong phòng thí nghiệm.
Ví dụ thí nghiệm 1 yếu tố: Ảnh hưởng của các chất điều hòa sinh trưởng BA lên khả năng nhân nhanh chồi in vitro cây hoa đồng tiền.

Hình 2. Sơ đồ thí nghiệm thiết kế kiểu CRD
(4 mức yếu tố chất điều hòa sinh trưởng 1, 2, 3, 4 với 3 lần lặp lại)
Ví dụ thí nghiệm 2 yếu tố: Ảnh hưởng của chất điều hòa sinh trưởng BA lên khả năng nhân nhanh chồi in vitro của 2 giống hoa đồng tiền.

Hình 3. Sơ đồ thí nghiệm thiết kế kiểu CRD
(8 nghiệm thức, 2 mức yếu tố A-Giống, 4 mức yếu tố B-Chất điều hòa sinh trưởng với, 3 lần lặp lại)
Bố trí kiểu khối đầy đủ ngẫu nhiên (RCBD/RCB)
Áp dụng khi số công thức thí nghiệm không quá lớn và có một hướng biến động (ví dụ: hướng phì nhiêu của đất, hướng di chuyển côn trùng, độ dốc của đồng ruộng,…). Từ đó, thiết kế các khối có kích thước bằng nhau, mỗi khối có chứa tất cả các công thức của một lần lặp lại. Kiểu sắp xếp RCBD được sử dụng nhiều trong nghiên cứu nông nghiệp.
Ví dụ: bố trí thí nghiệm khối hoàn toàn ngẫu nhiên để so sánh ảnh hưởng của mức độ bón phân đến năng suất của một giống lúa.
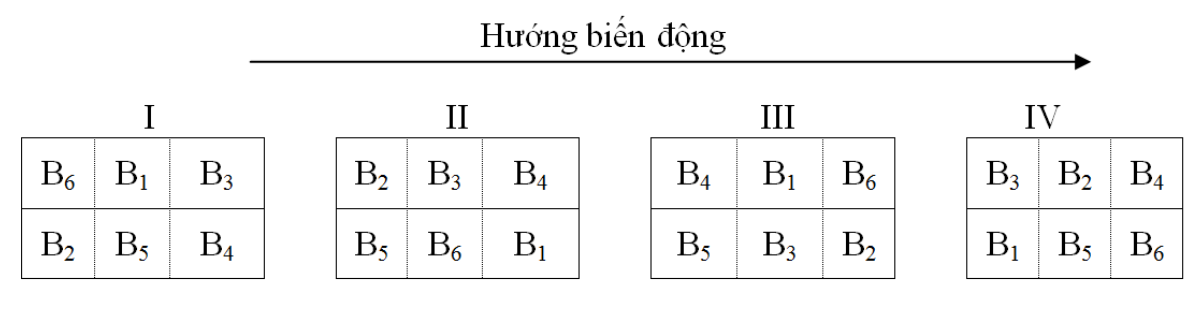
Hình 4. Sơ đồ thí nghiệm 1 yếu tố kiểu RCBD
(6 nghiệm thức, 6 mức yếu tố B-Phân bón với 4 lần lăp lại)
Ví dụ thí nghiệm với 2 yếu tố: bố trí thí nghiệm khối hoàn toàn ngẫu nhiên để so sánh ảnh hưởng mức độ bón phân đến năng suất của hai giống lúa.

Hình 5. Sơ đồ thí nghiệm 2 yếu tố kiểu RCBD
(10 nghiệm thức, 2 mức yếu tố A-Giống, 5 mức yếu tố B-Phân bón, 4 lần lăp lại)
Bố trí kiểu ô vuông Latinh (Latin Square D.)
Sử dụng cho thí nghiệm một yếu tố, khi có 2 nguồn biến động khác nhau giữa các thí nghiệm, thường gọi là hàng và cột. Mỗi hàng và mỗi cột là một khối đầy đủ chứa tất cả các nghiệm thức.
Ví dụ: So sánh năng suất 7 giống ớt lai được bố trí thí nghiệm theo kiểu ô vuông Latinh.
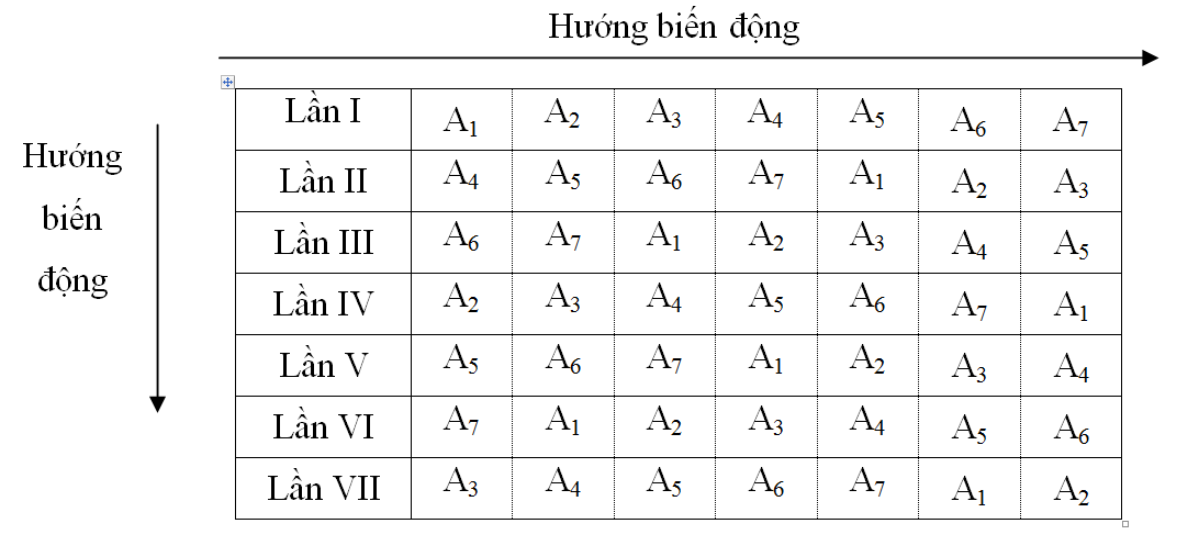
Hình 6. Sơ đồ kiểu ô vuông Latinh
(7 mức yếu tố A-Giống, 7 lần lặp lại)
Để đảm bảo yêu cầu mỗi công thức được nhắc lại một lần trên hàng hoặc trên cột, khi thiết kế thí nghiệm theo kiểu ô vuông Latinh thì số nghiệm thức thường lớn hơn 4 và nhỏ hơn 8. Bố trí thí nghiệm này ít được sử dụng rộng rãi trong nông nghiệp.
Bố trí kiểu chữ nhật Latinh (Latin Rectangular Square Design)
Sử dụng khi có 2 nguồn biến động khác nhau giữa các thí nghiệm, thường gọi là hàng và cột. Mỗi hàng và mỗi cột là một khối đầy đủ chứa tất cả các nghiệm thức và được sắp xếp theo hình chữ nhật.
Đây là dạng biến đổi từ kiểu bố trí ô vuông Latinh, số lượng ô trong thí nghiệm ít hơn so với kiểu ô vuông Latinh. Trong đó, số nghiệm thức (t) chia hết số hàng (r); số cột bằng số hàng (c=r); mỗi cột chính bằng t/r cột phụ.
Ví du: So sánh năng suất 9 giống lúa lai được bố trí theo kiểu chữ nhật Latinh 3x3x3.
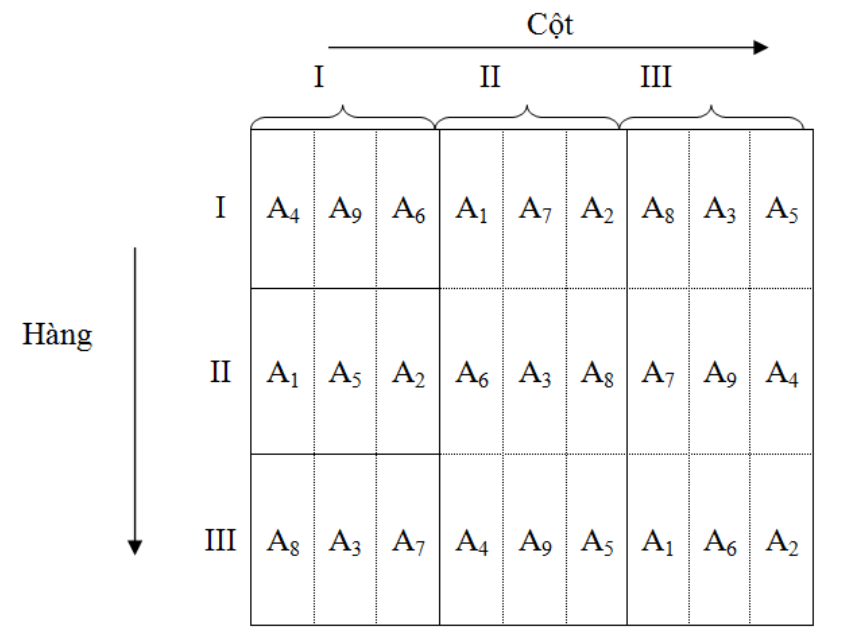
Hình 7. Sơ đồ kiểu chữ nhật Latinh 3x3x3
(9 mức yếu tố A-Giống, t=9, c=3, r=3, t/r=3)
Bố trí kiểu mạng lưới (Lattice Design)
Là kiểu bố trí dùng cho nhiều nghiệm thức, nhiều ô mà các nghiệm thức khác không bố trí được.
Đặc điểm: Hai nghiệm thức chỉ đứng cạnh nhau một lần trong một khối, các cặp đứng cạnh được so sánh cùng một độ chính xác. Bao gồm:
* Mạng lưới kiểu cân bằng (Balanced Lattices)
Số nghiệm thức là số chính phương (là số tự nhiên có căn bậc hai là một số tự nhiên), và số lần lặp lại của thí nghiệm sẽ phụ thuộc vào số nghiệm thức. Trong đó, số nghiệm thức là t=r2, số ô trong khối là c=r và số lần lặp lại là k=r+1. Tuy nhiên, với 36 nghiệm thức và 100 nghiệm thức trở lên thì không dùng mạng lưới kiểu cân bằng.
Bảng phân bố số nghiệm thức và số lần lặp lại:
| Số nghiệm thức (t) | 9 | 16 | 25 | 49 | 64 | 81 |
| Số ô trong khối (c) | 3 | 4 | 5 | 7 | 8 | 9 |
| Số lần lặp lại (k) | 4 | 5 | 6 | 8 | 9 | 10 |
Ví dụ thí nghiệm: Đánh giá năng suất 9 giống lúa mì.

Hình 8. Sơ đồ bố trị mạng cân bằng 3x3
(9 yếu tố A-Giống, t=9, c=3, k=4)
* Mạng lưới kiểu cân bằng từng phần (Parially Balanced Lattices)
Áp dụng cho nhiều nghiệm thức, với số lần lặp lại khá lớn. Phương pháp này giúp giảm số lần lặp lại của các nghiệm thức ở mạng lưới kiểu cân bằng. Nếu như ở thí nghiệm bố trí theo mạng lưới kiểu cân bằng cho 25 nghiệm thức cần 6 lần lặp lại, thì ở mạng cân bằng từng phần chỉ cần 2 lần lặp lại. Ngoài ra, phương pháp này còn cho phép bố trí 36 nghiệm thức và trên 100 nghiệm thức mà phương pháp mạng cần bằng không bố trí được. Mạng cân bằng từng phần bao gồm mạng đơn (2 lần lặp lại), mạng ba (3 lần lặp lại),...và mạng nhiều lần lặp lại.
Ví dụ thí nghiệm: Khảo sát 25 giống lúa lai F1.
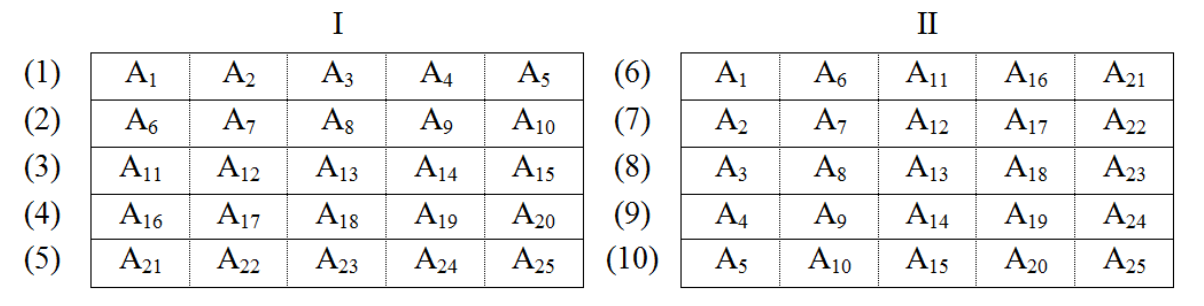
Hình 9. Sơ đồ bố trí mạng đơn cân bằng từng phần 5x5
(25 yếu tố A-Giống , t=25, c=5, k=2)
Bố trí kiểu mạng lưới vuông (Lattice, Squares)
Trong kiểu mạng lưới vuông, số nghiệm thức là số chính phương. Các hàng và các cột ở mỗi lần lặp lại được điều chỉnh sao cho nghiệm thức không cùng nằm trong một hàng hoặc một cột. Áp dụng mạng lưới vuông cho 9, 25, 49, 81, 121 và 169 nghiệm thức. Theo phương pháp này, số nghiệm thức t=r2, số lần lặp lại là k=(r+1)/2, số lần để 2 nghiệm thức cùng có mặt trên một hàng hoặc một cột là λ.
Ví dụ thí nghiệm: Năng suất quả/cây của 25 giống bông trong thí nghiệm bố trí mạng lưới vuông.
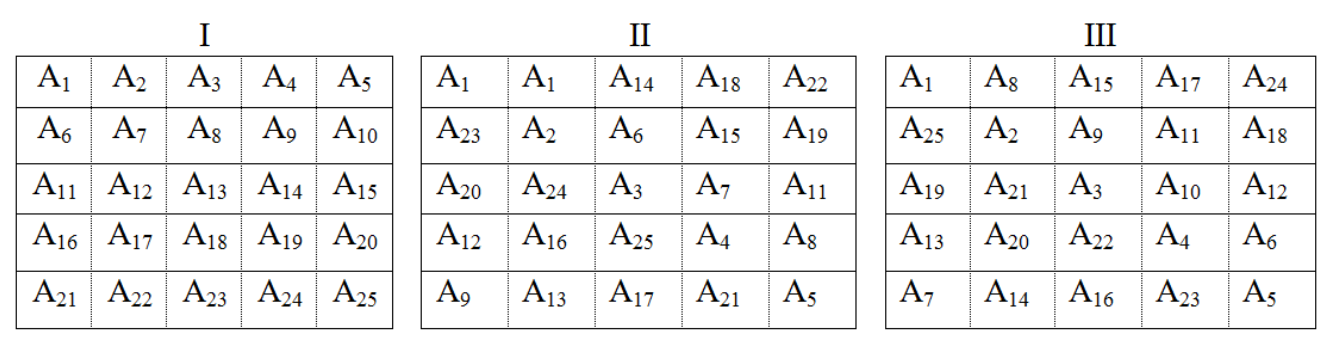
Hình 10. Sơ đồ lưới vuông cân bằng 5x5
(25 yếu tố A-Giống, t=25, k=3, λ=1)
Bố trí kiểu lô phụ (Split – Plot Design)
Áp dụng cho thí nghiệm hai yếu tố (không sử dụng cho thí nghiệm một yếu tố). Đây là cách bố trí thí nghiệm hỗ trợ cho phương pháp khối hoàn toàn khẫu nhiên (RCBD). Ở thí nghiệm hai yếu tố theo kiểu RCBD (Hình 5), mỗi nghiệm thức nằm ngẫu nhiên ở các vị trí khác nhau trong một lần lặp lại. Tuy nhiên, trong nhiều trường hợp, khi sử dụng phương pháp RCBD, có nghiệm thức bị ảnh hưởng bởi các yếu tố nghiên cứu từ ô bên cạnh, làm sai lệch kết quả. Do đó, nên sử dụng bố trí kiểu lô phụ: một trong hai yếu tố sẽ được coi là yếu tố phụ và được bố trí thành các lô chính, còn yếu tố còn lại (được xem là yếu tố chính) thì bố trí thành các lô phụ.
Ví dụ: theo thí nghiệm ở hình 5, nhưng muốn nghiên cứu ảnh hưởng của 5 mức độ bón phân đạm đến 3 giống lúa, để áp dụng bố trí kiểu lô phụ, người ta coi phân đạm là yếu tố phụ (bố trí thành lô chính), giống lúa là yếu tố chính (bố trí thành lô phụ).

Hình 11. Sơ đồ thí nghiệm kiểu lô phụ 5x3
(5 mức yếu tố A-Phân bón đạm (lô chính), 3 mức yếu tố B-Giống (lô phụ), 3 lần lặp lại)
Trong kiểu bố trí này, thứ tự các ô phụ (B1-B3) trong lô chính (A1-A5) thay đổi nên loại trừ được khác biệt giữa các lô chính.
Bố trí kiểu lô sọc/lô ngang (Strip – Plot Design)
Đây là kiểu bố trí đặc biệt của thí nghiệm hai yếu tố, có độ chính xác cao hơn so với bố trí kiểu lô phụ. Theo kiểu bố trí này, thứ tự các ô trong lô dọc và lô ngang không thay đổi nên loại trừ được khác biệt giữa các lô chính và lô phụ.
Ví dụ: Nghiên cứu ảnh hưởng 5 mức độ bón phân đạm đến 3 giống lúa kiểu lô sọc/lô ngang.

Hình 12. Sơ đồ kiểu lô sọc 5x3
(5 mức yếu tố A-Phân bón đạm, 3 mức yếu tố B-Giống, 3 lần lặp lại)
Bố trí phối hợp lô phụ – lô sọc (Strip Split – Plot Design)
Áp dụng cho thí nghiệm ba yếu tố. Bố trí phối hợp lô phụ - lô sọc là kiểu mở rộng theo cách bố trí kiểu lô sọc. Trong đó, ở các ô là khu vực giao nhau giữa các lô sọc và lô ngang sẽ bố trí yếu tố thứ ba.
Ví dụ: Thí nghiệm năng suất lúa bố trí kiểu lô phụ - lô sọc.

Hình 13. Sơ đồ bố trí lô phụ - lô sọc 3x6x2
(3 mức yếu tố A- Phân bón đạm, 6 mức yếu tố B-Giống, 2 mức yếu tố P-Lân, 3 lần lặp lại)
Việc lựa chọn phương pháp bố trí thí nghiệm phù hợp cho từng nghiên cứu sẽ giúp hạn chế sai số thí nghiệm không đáng có, là căn cứ cho các kết luận chính xác hơn về tác động của các yếu tố thí nghiệm. Đây cũng là cơ sở để có thể áp dụng tốt kết quả nghiên cứu vào thực tế sản xuất, kinh doanh.
Vân Anh tổng hợp
----------------------------------------
Tài liệu tham khảo:
[1] Phan Thanh Kiếm. Cơ sở toán học của các phép xử lý thống kê trong nghiên cứu khoa học nông nghiệp. NXB Nông nghiệp.
[2] Nguyễn Thị Lam, Phạm Tiến Dũng. Giáo trình phương pháp thí nghiệm. Hà Nội, 2005.
---------------------------------------------------------------------------------------------------
