Với bộ dữ liệu có từ hai biến định lượng trở lên, ta có thể hình dung mối tương quan của các biến thông qua hình ảnh trực quan từ các dạng biểu đồ phân tán (scatter plots), biểu đồ bong bóng (bubble chart), ma trận phân tán (scatterplot matrix) hay biểu đồ tương quan (correlogram). Ngoài ra, khi bộ dữ liệu có số lượng biến quá nhiều, việc giảm kích thước thông qua phân tích thành phần chính (PCA) được xem là phương pháp hữu hiệu.
1. Biểu đồ phân tán (scatter plots)
Biểu đồ phân tán (scatter plots hay scatter diagram) là một loại biểu đồ sử dụng tọa độ Descartes để hiển thị giá trị và mối quan hệ giữa hai biến định lượng cho một tập dữ liệu. Dữ liệu được hiển thị dưới dạng tập hợp các điểm, mỗi điểm có giá trị của một biến xác định vị trí trên trục hoành và giá trị của biến khác xác định vị trí trên trục tung. Biểu đồ phân tán là một trong 7 công cụ cơ bản của kiểm soát chất lượng trong doanh nghiệp (Hình 1).

Hình 1. 7 công cụ kiểm soát chất lượng (Nguồn: Viện Năng suất Việt Nam - VNPI)
Biểu đồ phân tán có thể được dùng khi 2 biến định lượng độc lập hoặc có một biến phụ thuộc vào biến còn lại. Trong trường hợp phụ thuộc, biến phụ thuộc (biến được dự đoán) thường được vẽ dọc theo trục tung, biến độc lập (biến dùng để đưa ra dự đoán) được vẽ dọc theo trục hoành. Trong trường hợp cả 2 biến độc lập với nhau, mỗi biến được vẽ ở một trục. Biểu đồ phân tán sẽ chỉ minh họa mức độ tương quan (không phải quan hệ nhân quả) giữa hai biến.
Ví dụ minh họa trong Hình 2 dưới đây thể hiện mối tương quan giữa 2 biến định lượng độc lập với nhau: chiều dài đầu (mm) và khối lượng cơ thể (g) của 123 con chim blue jay. Dễ dàng nhận thấy sự tương quan thuận chiều giữa chiều dài đầu với khối lượng cơ thể. Con chim có đầu dài nhất gần với khối lượng cơ thể tối đa quan sát được và con chim có đầu ngắn nhất gần với khối lượng cơ thể tối thiểu quan sát được.
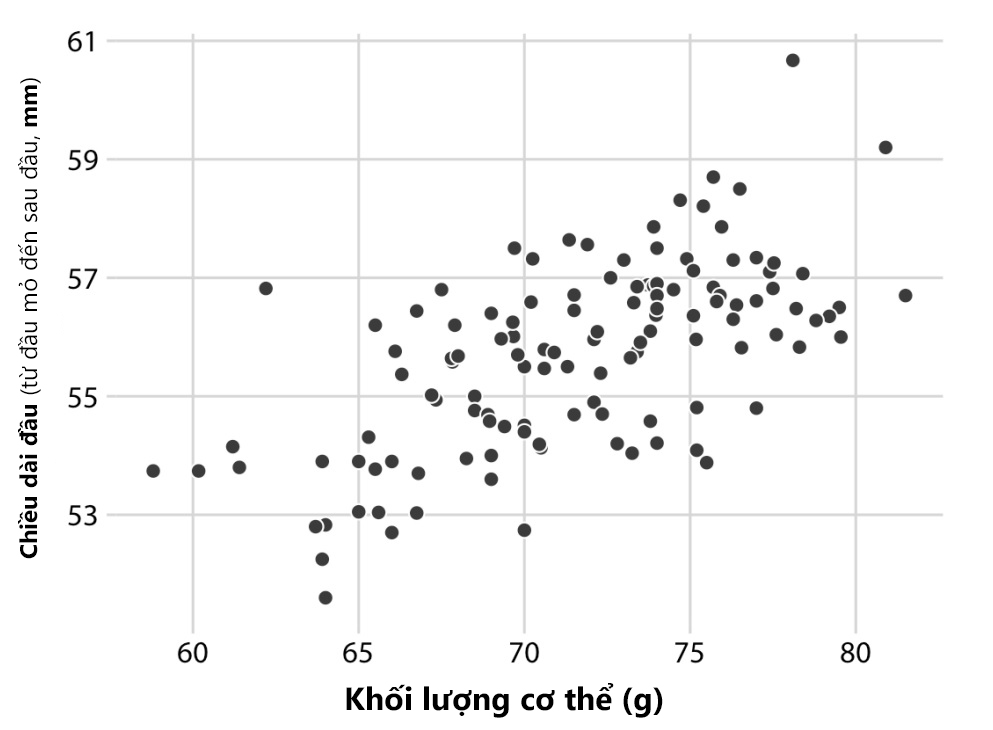
Hình 2. Biểu đồ phân tán về mối tương quan giữa chiều dài đầu và khối lượng cơ thể của 123 con chim blue jay (Nguồn: Fundamentals of Data Visualization (Wike, 2019))
Ta có thể sử dụng thêm biến phân loại để phân tích sự khác biệt giữa chim đực và cái (Hình 3). Có thể thấy trong biểu đồ, ở cùng một khối lượng cơ thể, con mái có xu hướng có đầu ngắn hơn con đực, đồng thời trọng lượng của chim cái cũng nhẹ hơn chim đực.
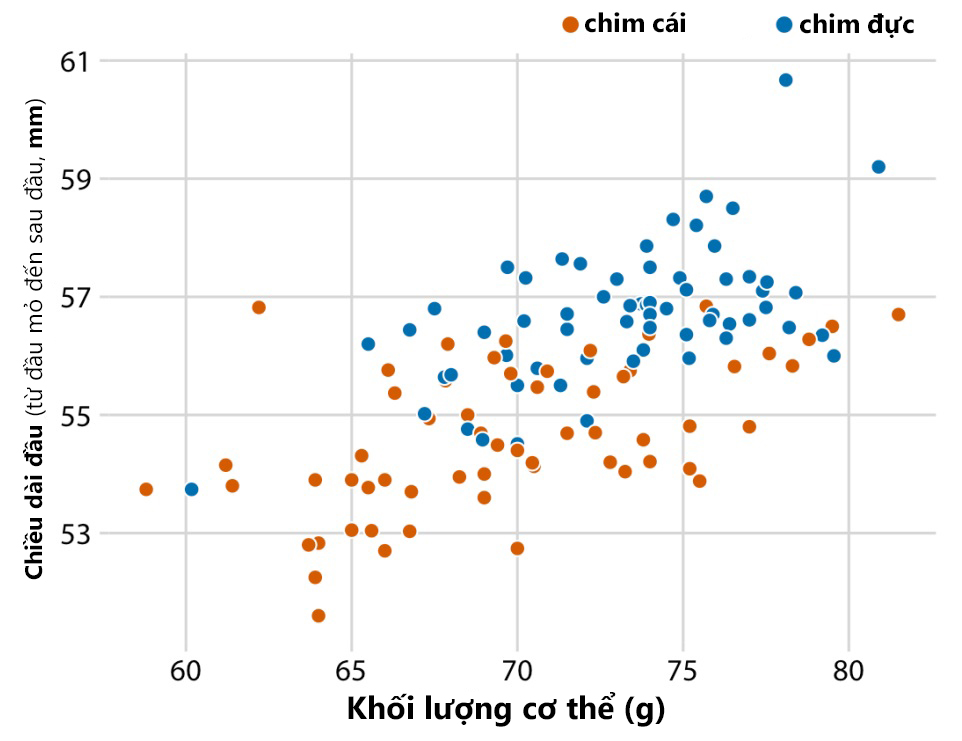
Hình 3. Biểu đồ phân tán về mối tương quan giữa chiều dài đầu và khối lượng cơ thể của 123 con chim blue jay, phân loại theo chim đực và cái (Nguồn: Fundamentals of Data Visualization (Wike, 2019))
Biểu đồ phân tán có thể gợi ý nhiều loại tương quan giữa các biến với một khoảng tin cậy nhất định. Các mối tương quan có thể là tích cực, tiêu cực, hoặc không có bất kỳ tương quan nào (Hình 4). Để đo lường độ mạnh liên kết giữa hai biến định lượng liên tục, hệ số tương quan Pearson là thang đo thường được sử dụng (Chi tiết về hệ số tương quan Pearson tham khảo trong bài viết “Thống kê mô tả trong nghiên cứu – Các đại lượng về sự tương quan”)
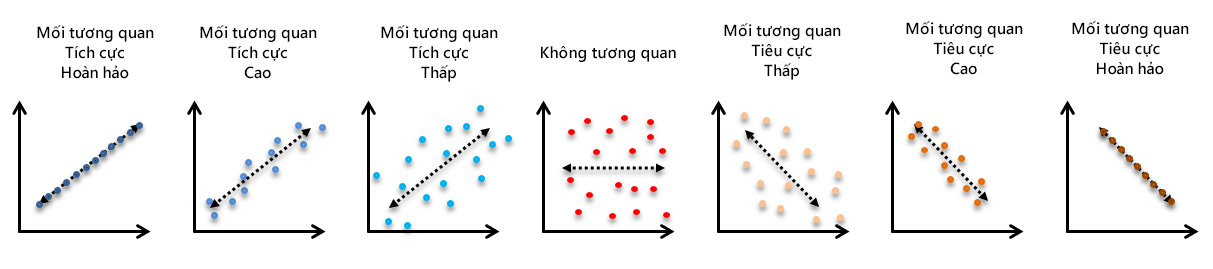
Hình 4. Các mối tương quan giữa 2 biến định lượng được thể hiện qua biểu đồ phân tán (Nguồn:medium.com)
Trong mô hình hồi quy tuyến tính, biểu đồ phân tán được sử dụng để kiểm định mối liên hệ tuyến tính giữa biến phụ thuộc với các biến độc lập. Giả định này sẽ được kiểm tra bằng biểu đồ phân tán giữa các phần dư chuẩn hóa trên trục tung và giá trị dự đoán chuẩn hóa trên trục hoành. Nếu kết quả cho thấy các giá trị phần dư được rải ngẫu nhiên xung quanh tung độ 0 và hình dạng tạo thành một đường thẳng thì giả định liên hệ tuyến tính không bị vi phạm Hình 5).
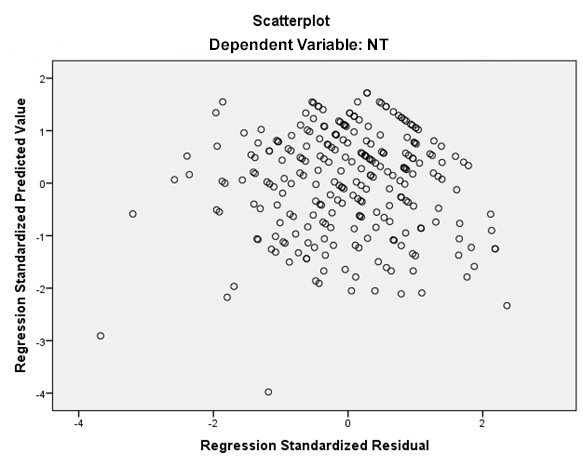
Hình 5. Biểu đồ phân tán giữa các phần dư và giá trị dự đoán
2. Biểu đồ bong bóng (bubble chart)
Biểu đồ bong bóng (bubble chart) có thể xem là một biến thể của biểu đồ phân tán, nhưng có thêm giá trị định lượng thứ ba. Trong đó, 2 giá trị được biểu diễn thông qua vị trí trục tung và trục hoành, giá trị còn lại được biểu diễn bằng kích thước của điểm dữ liệu.
Ví dụ về biểu đồ bong bóng trong Hình 6 minh họa mối quan hệ giữa 3 biến định lượng: GDP bình quân đầu người (trục hoành, đơn vị tính: 2.000$); Tuổi thọ (trục tung, đơn vị tính: năm) và dân số (kích thước bong bóng, đơn vị tính: người), theo 117 quốc gia tại 5 châu lục. Có thể dễ dàng nhận thấy châu Mỹ, châu Âu và châu Đại Dương có tuổi thọ cao hơn và GDP bình quân đầu người lớn hơn hầu hết các quốc gia ở châu Á và châu Phi.
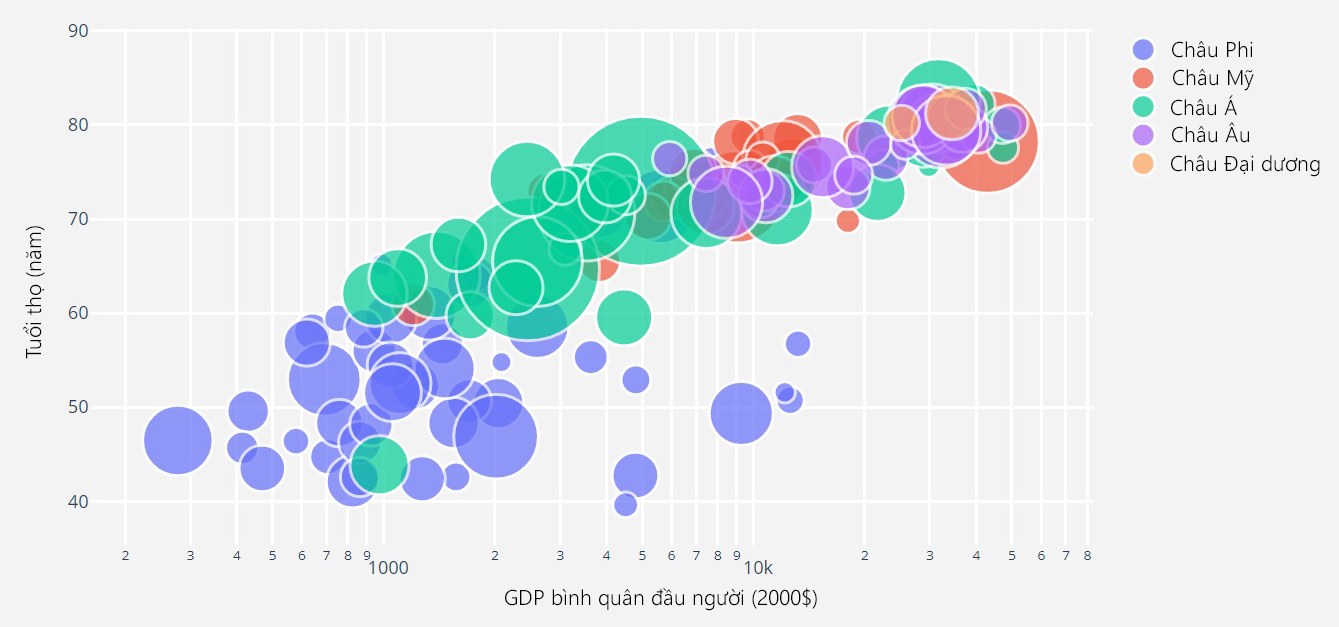
Hình 6. Biểu đồ bong bóng về mối tương quan giữa tuổi thọ, GDP bình quân đầu người và dân số của 117 quốc gia năm 2007, được phân loại màu sắc theo 5 châu lục (Nguồn: plotly.com)
Trong biểu đồ trên, ta chỉ có thể hình dung được những thông tin chung nhất về mối tương quan giữa tuổi thọ và GDP bình quân đầu người theo các châu lục và sự chênh lệch về dân số thông qua các bong bóng. Tuy nhiên, không rõ cụ thể bong bóng nào là của quốc gia nào và mối tương quan giữa tuổi thọ, GDP bình quân đầu người với dân số của các quốc gia đó.
Xem xét thêm ví dụ về 123 con chim blue jay ở mục 1 sau khi được bổ sung thêm biến kích thước hộp sọ (mm) vào bộ dữ liệu và tách giới tính ra 2 biểu đồ khác nhau (Hình 7). Do kích thước hộp sọ có sự chênh lệch không quá lớn, nên chênh lệch giữa các bong bóng không quá khác biệt. Ngoài ra, giống với ví dụ ở Hình 6, khó để xác định mối quan hệ giữa hộp sọ với khối lượng cơ thể hoặc chiều dài đầu.
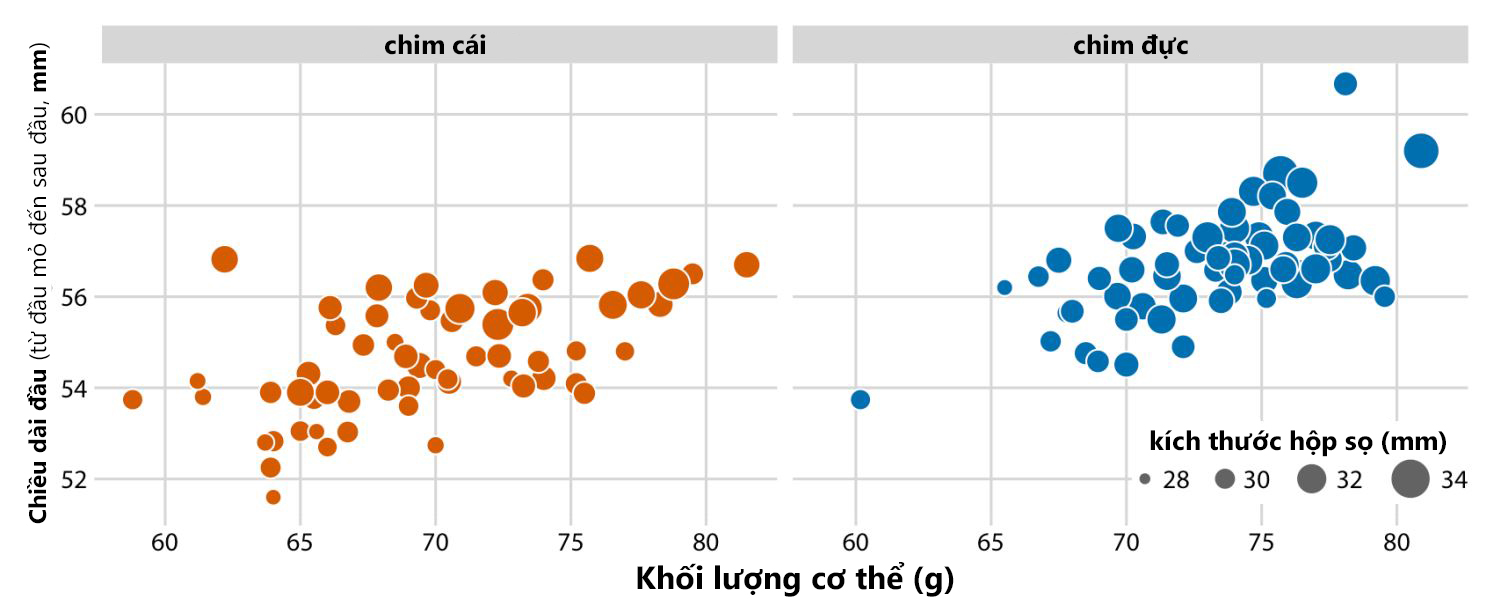
Hình 7. Biểu đồ bong bóng về mối tương quan giữa chiều dài đầu, khối lượng cơ thể và kích thước hộp sọ của 123 con chim blue jay, phân loại chim đực và cái theo màu sắc (Nguồn: Fundamentals of Data Visualization (Wike, 2019))
Qua các ví dụ trên, mặc dù lý tưởng để biển diễn nhiều biến cùng lúc trên một biểu đồ duy nhất, nhưng trong trường hợp lượng dữ liệu quá lớn hay sự chênh lệnh của bong bóng quá nhỏ, người phân tích phải mất thời gian để giải thích tất cả cấu trúc của biểu đồ cho người xem rồi mới có thể đưa ra kết luận cuối cùng. Ngoài ra, rất khó để xác định mối quan hệ giữa các biến trên trục và kích thước bong bóng. Do đó, để dễ giải thích kết quả chi tiết hơn theo định hướng bài phân tích, ta có thể bổ sung thêm các dạng biểu đồ khác, hoặc phân tích tương quan cụ thể giữa các biến định lượng sử dụng ma trận biểu đồ phân tán (scatterplot matrix).
3. Ma trận biểu đồ phân tán (scatterplot matrix)
Ma trận biểu đồ phân tán là một tập hợp các biểu đồ phân tán cho biết các biến định lượng trong bộ dữ liệu có liên quan như thế nào với nhau. Sau khi biểu diễn tất cả các kết hợp hai chiều của các biến, ma trận có thể hiển thị mối quan hệ giữa các biến để làm nổi bật mối quan hệ nào có thể là quan trọng.
Từ ví dụ ở Hình 7, tách 3 biến định lượng chiều dài đầu, khối lượng cơ thể và kích thước hộp sọ của 123 con chim blue jay thành một ma trận 3 cột 3 dòng để biểu diễn mối quan hệ của từng cặp biến định lượng với nhau (Hình 8). Có thể thấy, tương quan giữa kích thước hộp sọ và hai biến khác dễ dàng nhận thấy trong các biểu đồ phân tán theo cặp. Trong đó, mối quan hệ giữa kích thước hộp sọ và khối lượng cơ thể giữa chim cái và chim đực có thể so sánh được, chim cái có xu hướng kích thước hộp sọ nhỏ hơn.
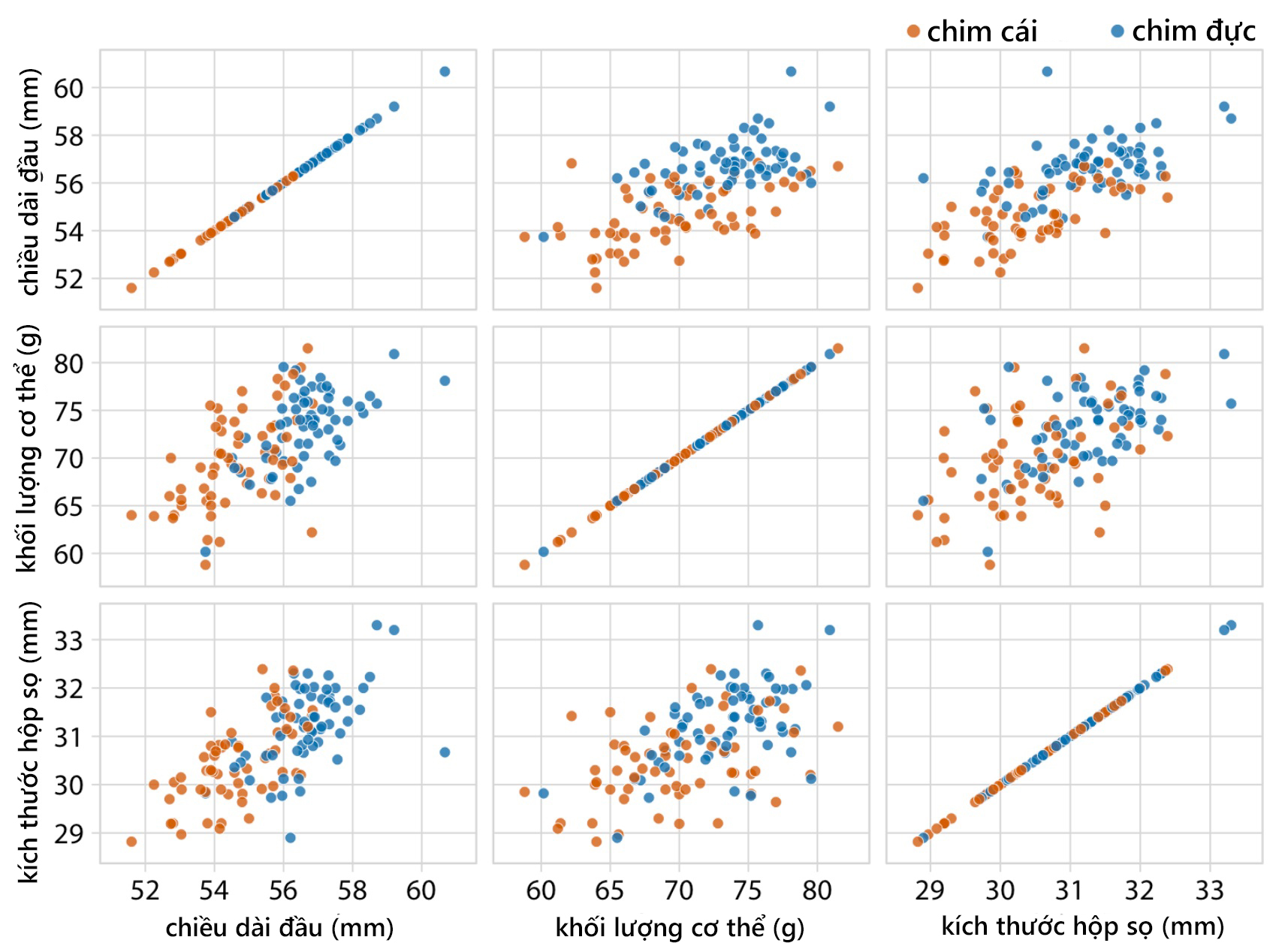
Hình 8. Ma trận biểu đồ phân tán về mối tương quan giữa chiều dài đầu, khối lượng cơ thể và kích thước hộp sọ của 123 con chim blue jay, phân loại theo chim đực và cái (Nguồn: Fundamentals of Data Visualization (Wike, 2019))
4. Biểu đồ tương quan (Correlogram)
Trong trường hợp có từ 3 đến 4 biến định lượng trở lên, thay vì biểu diễn trực quan tất cả dữ liệu của các biến định lượng lên biểu đồ, ta có thể tính toán hệ số tương quan Pearson giữa từng cặp biến và trực quan số liệu này lên biểu đồ. Phương pháp này được gọi là trực quan bằng biểu đồ tương quan Correlogram. Biểu đồ sử dụng một dải màu để chỉ ra các giá trị hệ số tương quan trong khoảng từ [-1;1].
Ví dụ trong Hình 9 minh họa 1 biểu đồ tương quan Correlogram sử dụng một tập dữ liệu gồm 214 mảnh thủy tinh và thành phần hóa học trong đó, tạo thành 21 cặp tương quan hiển thị cùng một lúc dưới dạng ma trận các ô màu, mỗi ô biểu thị một hệ số tương quan.
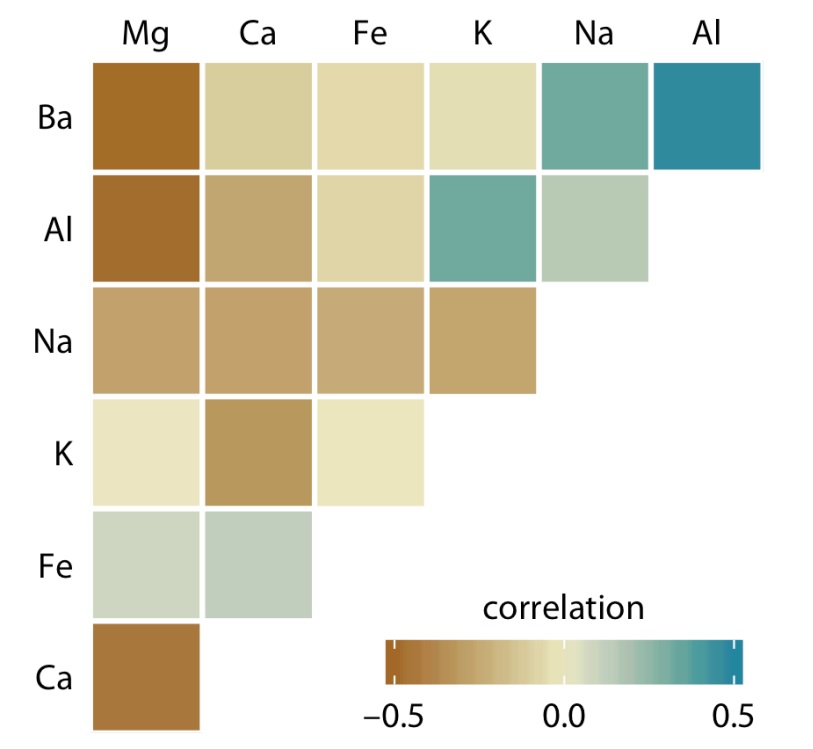
Hình 9. Mối tương quan về hàm lượng khoáng chất được biểu diễn bằng các ô vuông theo dải màu tương ứng với hệ số tương quan (Nguồn: Fundamentals of Data Visualization (Wike, 2019))
Theo dải màu, các hình vuông đậm cho thấy sự tương quan cao, các ô nhạt cho thấy sự tương quan thấp. Tuy nhiên, cách biểu diễn này chưa tối ưu do các tương quan thấp không bị triệt tiêu một cách trực quan. Phương pháp tối ưu hơn là hiển thị các mối tương quan dưới dạng các vòng tròn màu và chia tỷ lệ kích thước vòng tròn tương ứng với giá trị tuyệt đối của hệ số tương quan (Hình 10).
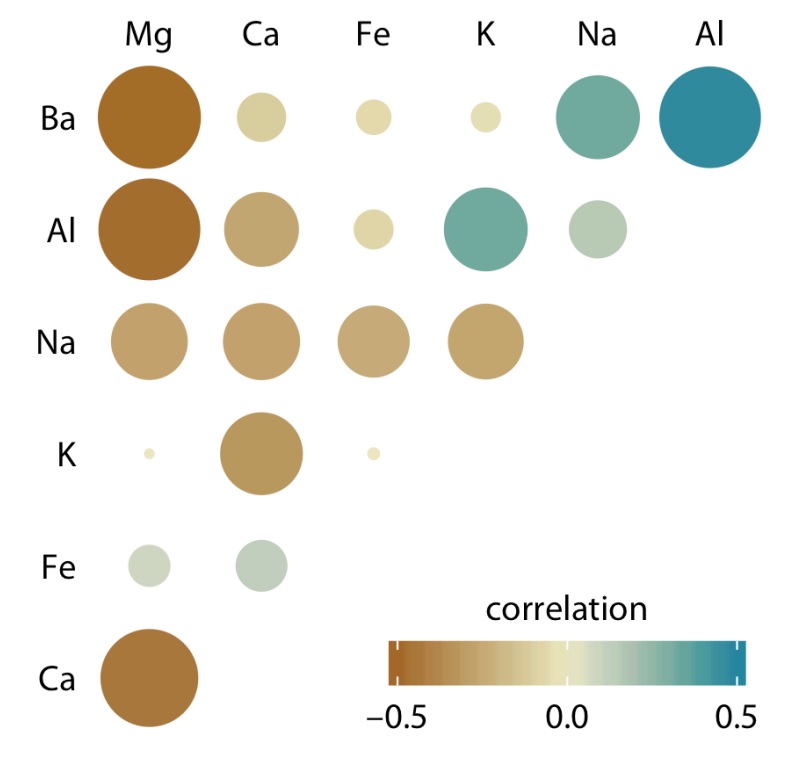
Hình 10. Mối tương quan về hàm lượng khoáng chất được biểu diễn bằng các ô tròn theo dải màu và kích thước tương ứng với hệ số tương quan (Nguồn: Fundamentals of Data Visualization (Wike, 2019))
Việc trực quan bằng biểu đồ tương quan Correlogram khá trừu tượng vì dữ liệu thô đã được tính toán và sự tương quan chỉ được thể hiện thông qua độ lớn của hệ số tương quan, không cung cấp thêm thông tin về mối quan hệ, khiến cho kết luận được đưa ra từ thông tin trên biểu đồ có thể không đầy đủ. Phương pháp giảm số chiều dữ liệu (mục kế tiếp) cho phép hiển thị đầy đủ hơn thông tin về dữ liệu thô, cũng như mối tương quan giữa nhiều biến định lượng.
5. Phương pháp giảm số chiều dữ liệu (Principal Component Analysis)
Phân tích thành phần chính (Principal Components Analysis - PCA) là một thuật toán thống kê được sử dụng rộng rãi nhất trong việc giảm kích thước của một tập dữ liệu. Phương pháp PCA được giới thiệu lần đầu tiên bởi Karl Pearson vào năm 1901, được Harold Hotelling phát triển độc lập và đặt tên vào những năm 1930.
Ý tưởng chính của phương pháp PCA là giảm kích thước của một tập dữ liệu gồm một lượng lớn các biến có liên quan lẫn nhau, đồng thời, giữ lại càng nhiều càng tốt sự biến thiên trong tập dữ liệu. Sự giảm thiểu này đạt được bằng cách chuyển đổi thành một tập hợp các biến mới, các thành phần chính (PC) bằng sự kết hợp tuyến tính các biến ban đầu trong dữ liệu, được chuẩn hóa về giá trị trung bình bằng 0 và phương sai đơn vị. Các PC được chọn sao cho chúng không có mối liên hệ với nhau và chúng được sắp xếp sao cho thành phần đầu tiên nắm bắt được lượng biến động lớn nhất có thể trong dữ liệu và các thành phần tiếp theo nắm bắt ngày càng ít hơn. Thông thường, các tính năng chính trong dữ liệu chỉ có thể được nhìn thấy từ hai hoặc ba PC đầu tiên.
Nói một cách đơn giản hơn, phương pháp PCA sử dụng phép biến đổi trực giao để biến đổi một tập hợp dữ liệu từ một không gian nhiều chiều sang một không gian mới ít chiều hơn (2 hoặc 3 chiều) nhằm tối ưu hóa việc thể hiện sự biến thiên của dữ liệu.
Trong Hình 11 là ví dụ đơn giản khi sử dụng phương pháp PCA để biến đổi cho tập dữ liệu 2 chiều. Hình 11a là dữ liệu gốc ban đầu về mối quan hệ giữa chiều dài đầu và kích thước hộp sọ của 123 con chim blue jay, phân loại chim đực và cái theo màu sắc. Hình 11b là bước chia tỷ lệ các giá trị dữ liệu ban đầu thành giá trị trung bình = 0 và phương sai đơn vị. Tiếp đến là xác định các biến mới (các thành phần chính) dọc theo hướng của sự thay đổi tối đa trong dữ liệu. Hình 11c là bước cuối cùng, chiếu dữ liệu vào các tọa độ mới, phép chiếu này tương đương với phép quay của các điểm dữ liệu xung quanh điểm gốc, cụ thể ở đây là xoay 45 độ.
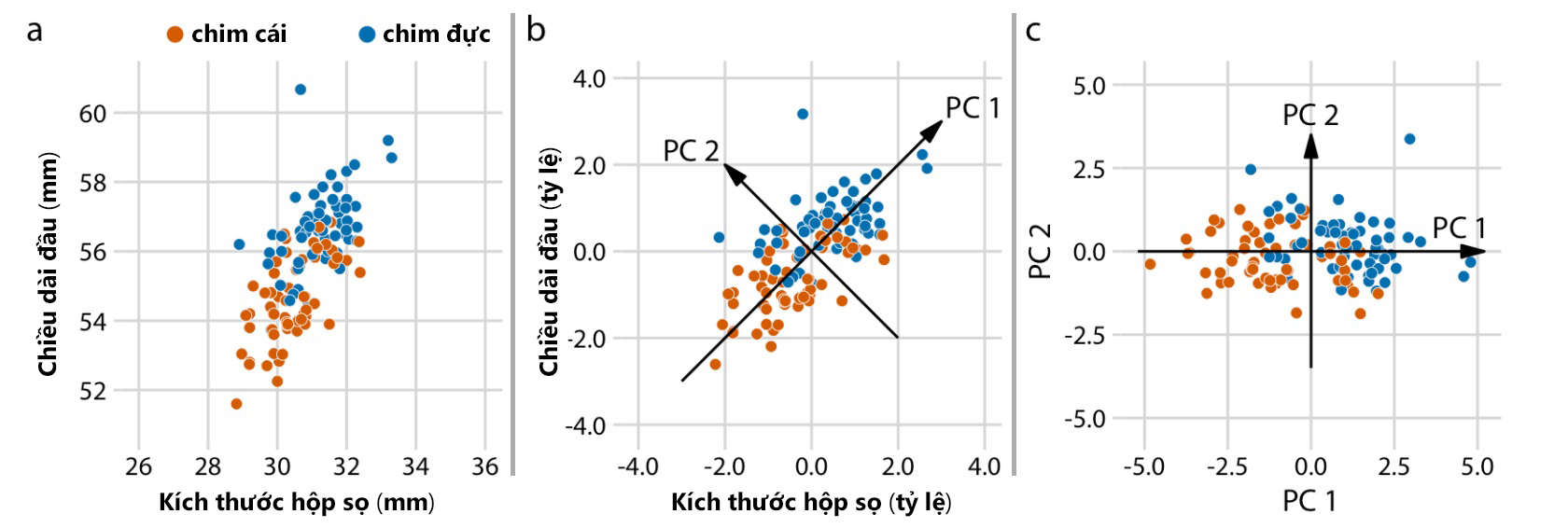
Hình 11. Ví dụ đơn giản về 3 bước thực hiện phân tích các thành phần chính theo hai chiều dữ liệu (Nguồn: Fundamentals of Data Visualization (Wike, 2019))
Trong ví dụ về thành phần hóa học có trong các mảnh thủy tinh, dữ liệu gốc ban đầu có đến 7 chiều dữ liệu thể hiện thông tin của 7 chất hóa học. Vì các PC là tổ hợp tuyến tính của các biến ban đầu (sau khi chuẩn hóa), 7 chất hóa học này có thể được biểu diễn dưới dạng mũi tên chỉ ra mức độ chúng đóng góp vào PC (Hình 12a). Thành phần một (PC1) chủ yếu đo lượng nhôm (Al), bari (Ba), natri (Na) và magiê (Mg) trong mảnh thủy tinh, thành phần hai (PC2) chủ yếu đo lượng canxi (Ca) và kali (K), và ở một mức độ nào đó là lượng nhôm (Al) và magiê (Mg). Độ dài ngắn của các mũi tên cho thấy có nhiều hơn hai PC trong bộ dữ liệu.
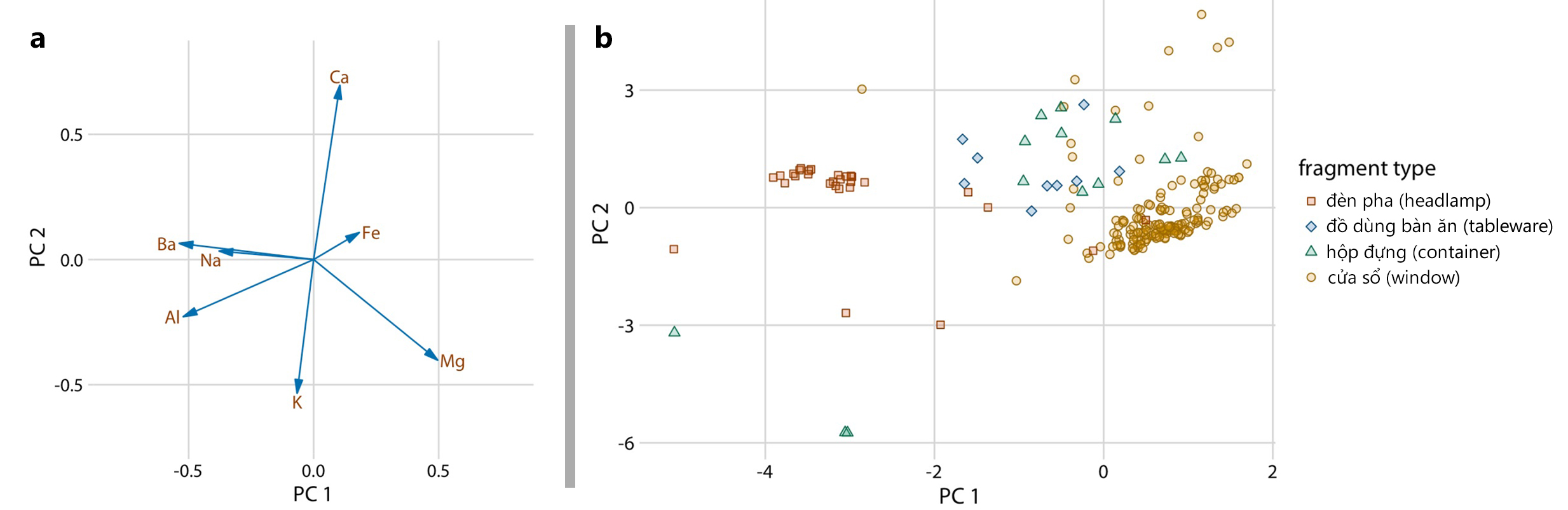
Hình 12. Phân tích theo 2 thành phần chính của bộ dữ liệu thành phần hóa học trong 214 mảnh thủy tinh (Nguồn: Fundamentals of Data Visualization (Wike, 2019))
Hình 12b là biểu đồ sau khi đưa dữ liệu gốc vào không gian các thành phần chính. Có thể thấy các mảnh thủy tin từ đèn pha (headlamp) và cửa sổ (window) tập trung vào các vùng được phân định rõ ràng, còn các mảnh thủy tinh từ đồ dùng đồ ăn (tableware) và hộp đựng (container) có xu hướng phân tán mạnh hơn. Ngoài ra, khi tiến hành so sánh với Hình 12a, có thể kết luận rằng các mảnh thủy tinh từ cửa sổ có xu hướng hàm lượng magiê cao hơn trung bình và thấp hơn hàm lượng bari, nhôm và natri trung bình; ngược lại hoàn toàn với các mảnh thủy tinh từ đèn pha. Bên cạnh đó, có thể thấy một số mảnh thủy tinh thuộc giá trị ngoại lệ (Outliers), khi có cả giá trị PC1 và giá trị PC2 âm, cho thấy mảnh thủy tinh này có thành phần khác biệt đáng kể so với tất cả các mảnh khác được phân tích.
***
Tất cả các dạng biểu đồ được giới thiệu ở trên đều có những ưu, nhược điểm riêng khi sử dụng biểu diễn trực quan dữ liệu. Để có thể sử dụng cho bài phân tích tương quan giữa các biến định lượng, không có dạng biểu đồ nào là tối ưu nhất, thay vào đó ta cần nắm rõ nội dung muốn diễn giải để áp dụng đúng dạng biểu đồ, mang đến thông tin hữu ích và dễ hiểu nhất cho người xem.
Duy Sang tổng hợp
----------------------------------------
Tài liệu tham khảo chính:
– Jarrell, S. B. (1994). Basic Statistics. William C Brown Communications.
– Jolliffe, I. (1986). Principal Component Analysis. Springer Science + Business Media, LLC.
– Wikipedia. (2021). Bubble chart. Retrieved from Wikipedia: https://en.wikipedia.org/wiki/Bubble_chart.
– Wikipedia. (2022). Principal component analysis. Retrieved from Wikipedia: https://en.wikipedia.org/wiki/Principal_component_analysis.
– Wikipedia. (2022). Scatter plot. Retrieved from Wikipedia: https://en.wikipedia.org/wiki/Scatter_plot.
– Wilke, C. O. (2019). Fundamentals of Data Visualization. O’Reilly Media.
----------------------------------------
Các bài viết liên quan:
Trực quan hóa dữ liệu – Phần 1: Tổng quan về biểu đồ
Trực quan hóa dữ liệu – Phần 2: Tổng quan về hệ trục tọa độ
Trực quan hóa dữ liệu – Phần 3: Một số dạng biểu đồ thể hiện độ lớn của dữ liệu
Trực quan hóa dữ liệu – Phần 4: Một số dạng biểu đồ thể hiện tỷ lệ của dữ liệu
Trực quan hóa dữ liệu – Phần 5: Các dạng biểu đồ thể hiện sự phân phối của dữ liệu
---------------------------------------------------------------------------------------------------
