Trực quan hình dạng phân phối của dữ liệu đóng vai trò quan trọng việc phân tích dữ liệu và so sánh mức độ tập trung dữ liệu giữa các nhóm. Trong đó, các dạng biểu đồ đơn giản và thường gặp nhất là Histogram và biểu đồ mật độ, ngoài ra còn có các dạng biểu đồ biểu diễn nhiều phân phối cùng lúc như biểu đồ hộp, violin và ridgeline.
1. Biểu đồ Histogram và biểu đồ mật độ
Biểu đồ Histogram được sử dụng để mô tả trực quan sự phân bố tần suất cho tập dữ liệu (đã được giới thiệu tại bài: Thống kê mô tả trong nghiên cứu – Các đại lượng về hình dáng phân phối), khá phổ biến, ít nhất từ thế kỷ 18, vì dễ được vẽ bằng tay (Wilke, 2019). Tuy nhiên, hiện biểu đồ Histogram đang dần bị thay thế bởi các biểu đồ mật độ, do những hạn chế khi so sánh sự phân bố của một biến trên nhiều danh mục.
Biểu đồ mật độ (Density plot)
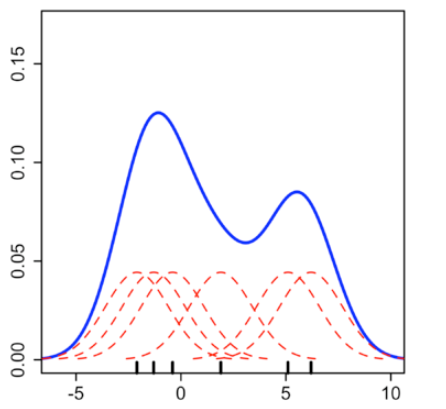
Biểu đồ mật độ biểu diễn dữ liệu liên tục bằng một đường cong được ước lượng từ dữ liệu với phương pháp ước lượng mật độ hạt nhân. Trong phương pháp này, một đường cong liên tục được vẽ tại mọi điểm dữ liệu riêng lẻ. Tất cả các đường cong này sẽ được cộng lại để tạo ra một đường ước tính mật độ duy nhất. Hạt nhân thường được sử dụng nhất là Gaussian (tạo ra đường cong hình chuông Gauss tại mỗi điểm dữ liệu). Trong Hình 1, mỗi đường thẳng đứng nhỏ màu đen trên trục x đại diện cho một điểm dữ liệu. Các hạt nhân riêng lẻ được vẽ bằng các đường đứt nét màu đỏ phía trên mỗi điểm. Đường cong màu xanh dương đậm được tạo ra bằng cách cộng các hạt nhân riêng lẻ và tạo thành biểu đồ mật độ tổng thể.
Hình 1. Biểu đồ mật độ (Nguồn: Wikipeadia)
Trục x là giá trị của biến, trục y là hàm mật độ xác suất để ước tính mật độ nhân. Tương tự với độ rộng cột trên biểu đồ Histogram, biểu đồ mật độ cũng có 1 tham số giúp xác định mức độ khái quát hoặc chi tiết của đường cong, gọi là bandwidth. Nếu bandwidth quá nhỏ, đường cong ước tính mật độ có thể trở nên quá nhọn và các xu hướng chính trong dữ liệu có thể bị che khuất. Nếu bandwidth quá lớn, thì các thông tin giá trị nhỏ hơn trong dữ liệu có thể biến mất (Hình 2).
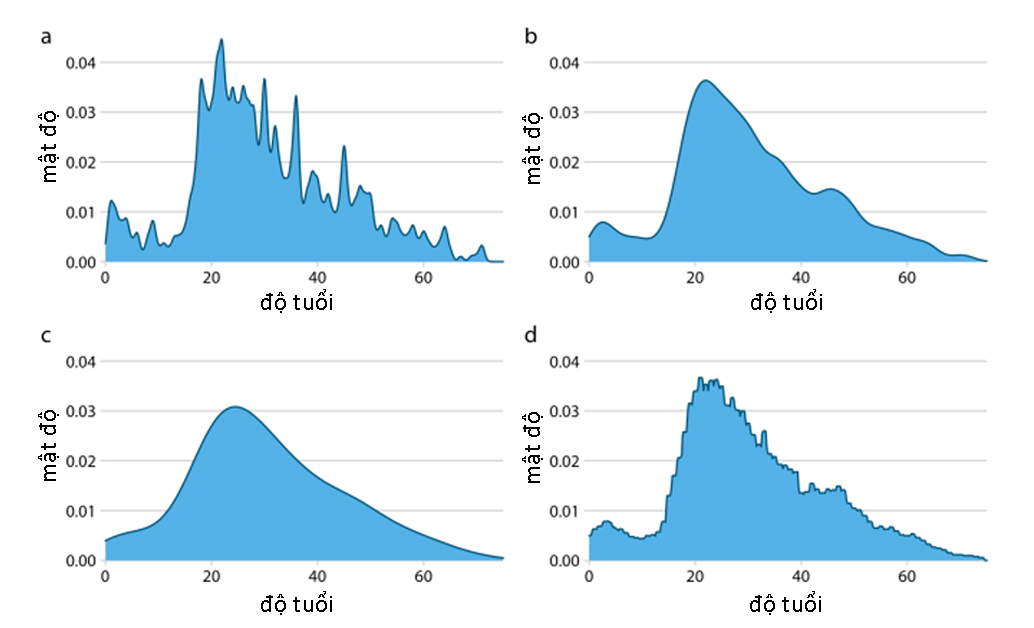
Hình 2. Minh họa 4 trường hợp biểu đồ mật độ theo hạt nhân và giá trị bandwidth
(Nguồn: Fundamentals of Data Visualization)
Trong Hình 2, phân bố cùng độ tuổi của một nhóm người được hiển thị theo 4 kết hợp khác nhau: (a) Hạt nhân Gaussian, bandwidth = 0,5; (b) Hạt nhân Gaussian, bandwidth = 2; (c) Hạt nhân Gaussian, bandwidth = 5; (d) Hạt nhân hình chữ nhật, bandwidth = 2. Có thể thấy, sự lựa chọn của hạt nhân ảnh hưởng đến hình dạng của đường cong mật độ: hạt nhân Gaussian sẽ có xu hướng tạo ra các hình dạng mật độ với chóp cong hình chuông và đuôi mịn; hạt nhân hình chữ nhật sẽ tạo ra hình dạng các bậc trên đường cong. Ngoài ra, càng có nhiều điểm dữ liệu trong tập dữ liệu, thì việc lựa chọn hạt nhân càng ít quan trọng, nên các biểu đồ mật độ có xu hướng đáng tin cậy và cung cấp nhiều thông tin đối với các tập dữ liệu lớn, nhưng lại có thể gây hiểu nhầm cho các tập dữ liệu chỉ một vài điểm.
Biểu diễn phân bố của một biến phân loại
Với 1 biến phân loại, hình dạng 2 biểu đồ gần như tương tự nhau và không khó để quan sát. Tuy nhiên, biểu đồ mật độ có xu hướng tạo ra sự xuất hiện của dữ liệu không tồn tại, đặc biệt là ở phần đuôi.
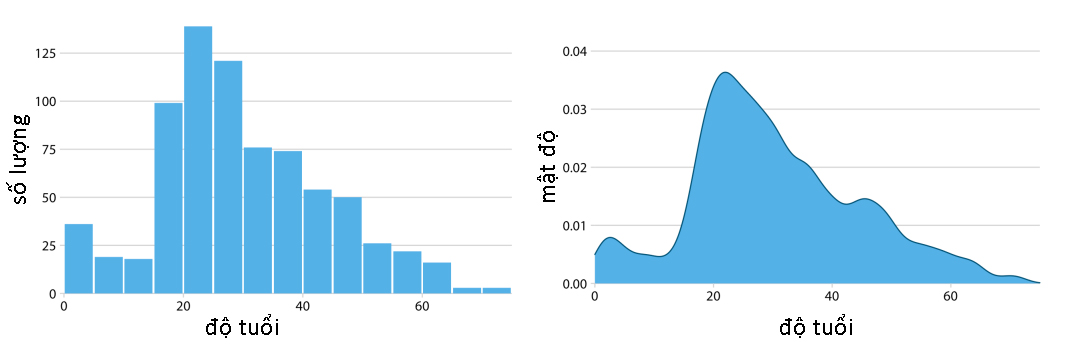
Hình 3. Trực quan độ tuổi theo biểu đồ Histogram và biểu đồ mật độ
(Nguồn: Fundamentals of Data Visualization)
Biểu diễn phân bố của nhiều biến cùng lúc
Khi dữ liệu có thêm 1 biến phân loại như giới tính, cách trực quan theo dạng xếp chồng lên nhau của biểu đồ mật độ trở nên tối ưu, với các đường liên tục giúp các phân bố tách biệt nhau và dễ quan sát hơn biểu đồ Histogram (Hình 4).
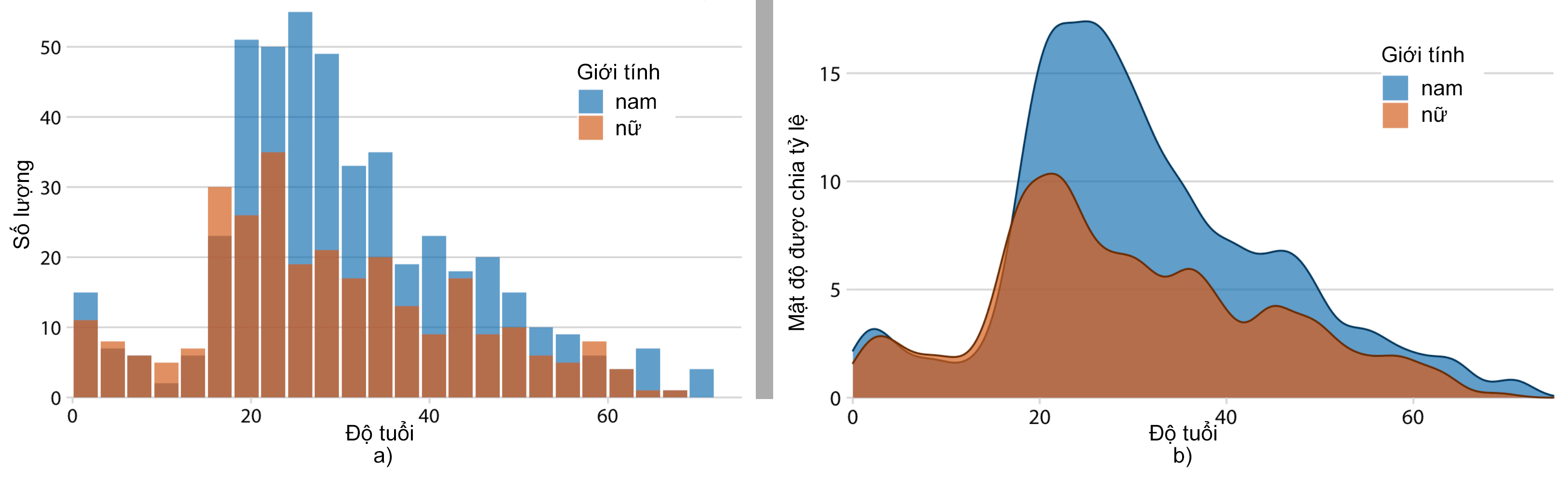
Hình 4. Trực quan độ tuổi và giới tính với biểu đồ Histogram(a) và biểu đồ mật độ(b)
(Nguồn: Fundamentals of Data Visualization)
Để so sánh phân bố tuổi của nam và nữ rõ ràng hơn, có thể tách biệt thành 2 biểu đồ và so sánh với phân bố tuổi của tổng thể (Hình 5). Cách trực quan này giúp người xem phân biệt rõ sự chênh lệch giữa 2 nhóm, cụ thể: trong độ tuổi từ 20 đến 50, số lượng nam nhiều hơn hẳn (có thể là gấp đôi) so với nữ; độ tuổi trên 70, giới tính chủ yếu là nam. Còn trong các độ tuổi còn lại, nam và nữ có tỷ lệ xấp xỉ bằng nhau.
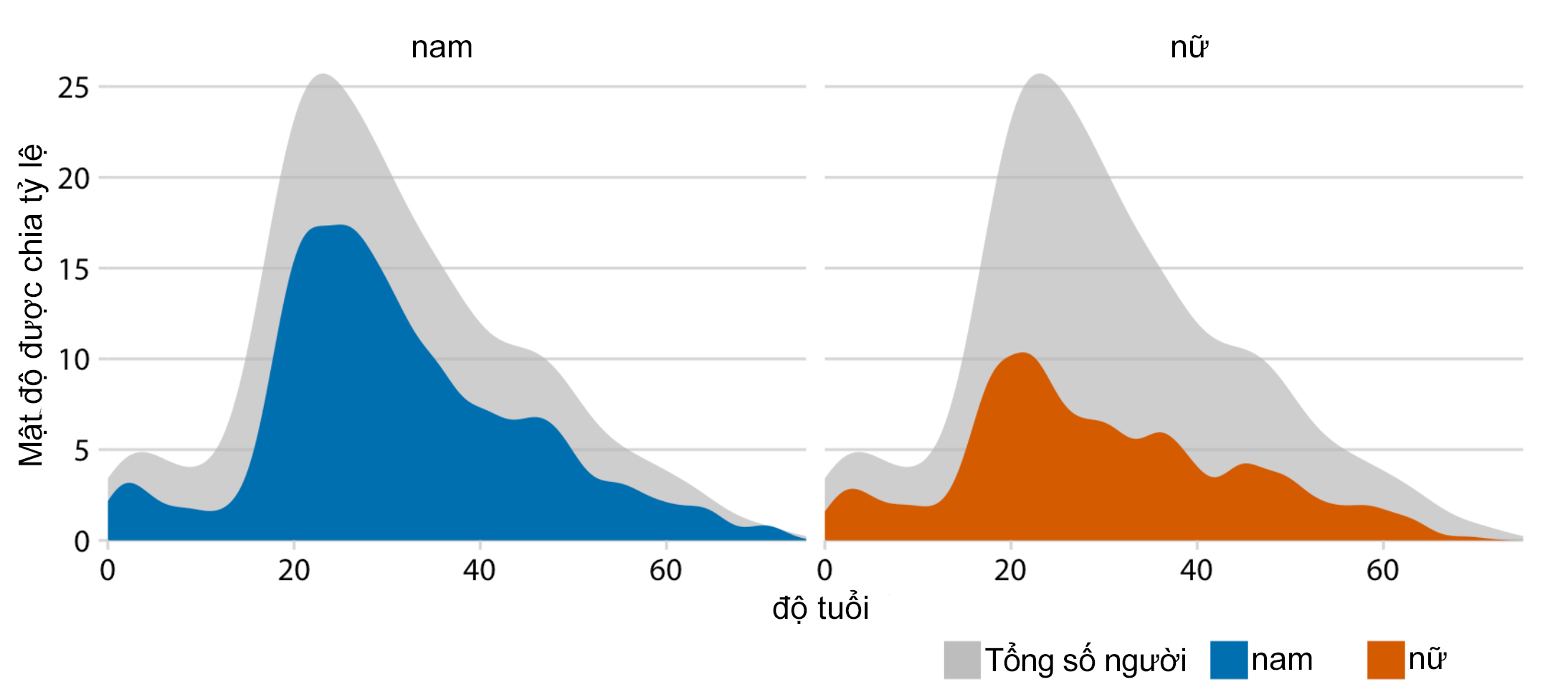
Hình 5. Trực quan độ tuổi riêng theo từng giới tính bẳng biểu đồ mật độ
(Nguồn: Fundamentals of Data Visualization)
Ngoài ra, trong trường hợp dữ liệu đạt được sự phân biệt, biểu đồ mật độ vẫn có thể biểu diễn tốt khi có nhiều hơn 2 biến phân loại. Chẳng hạn như để mô tả sự phân bố tỷ lệ chất béo trong sữa của 4 giống bò khác nhau, sử dụng biểu đồ mật độ cho đỉnh của 4 đường cong có sự tách biệt rõ ràng (Hình 6).
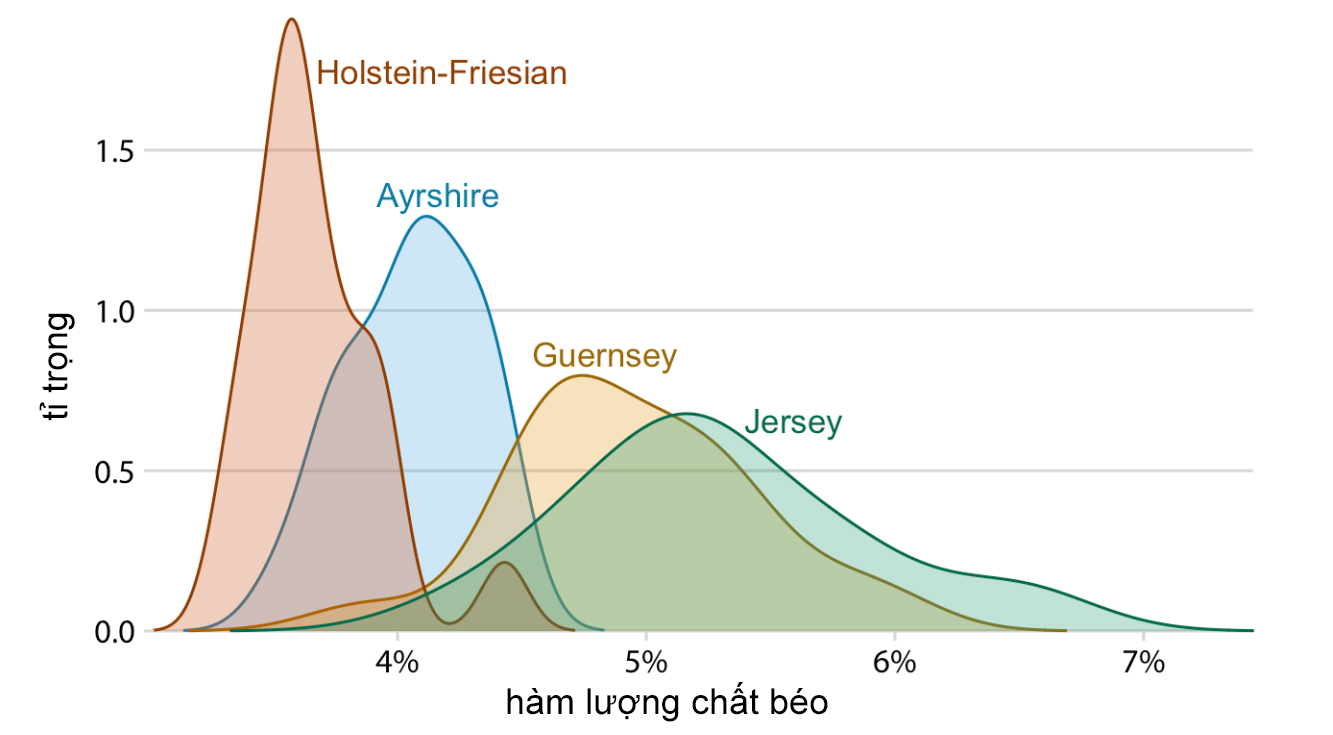
Hình 6. Trực quan hàm lượng chất béo của 4 giống bò bằng biểu đồ mật độ
(Nguồn: Fundamentals of Data Visualization)
2. Các dạng biểu đồ sử dụng cho trực quan nhiều phân phối cùng lúc
Trong trường hợp cần biểu diễn nhiều phân phối cùng lúc, chẳng hạn như sự biến đổi nhiệt độ theo 12 tháng trong năm, các dạng biểu đồ như trên sẽ không còn phù hợp. Khi đó, người ta sử dụng các biểu đồ phân phối như biểu đồ hộp (box plots), biểu đồ violin (violin plots) và biểu đồ ridgeline (ridgeline plots).
Biểu đồ hộp
Biểu đồ hộp (Box plots) được nhà thống kê John Tukey tạo ra vào đầu những năm 1970. Nó nhanh chóng trở nên phổ biến, vì dễ vẽ bằng tay và mang lại nhiều thông tin. Biểu đồ hộp chia dữ liệu thành các phần tư và hiển thị chúng theo cách chuẩn hóa (Hình 7a).
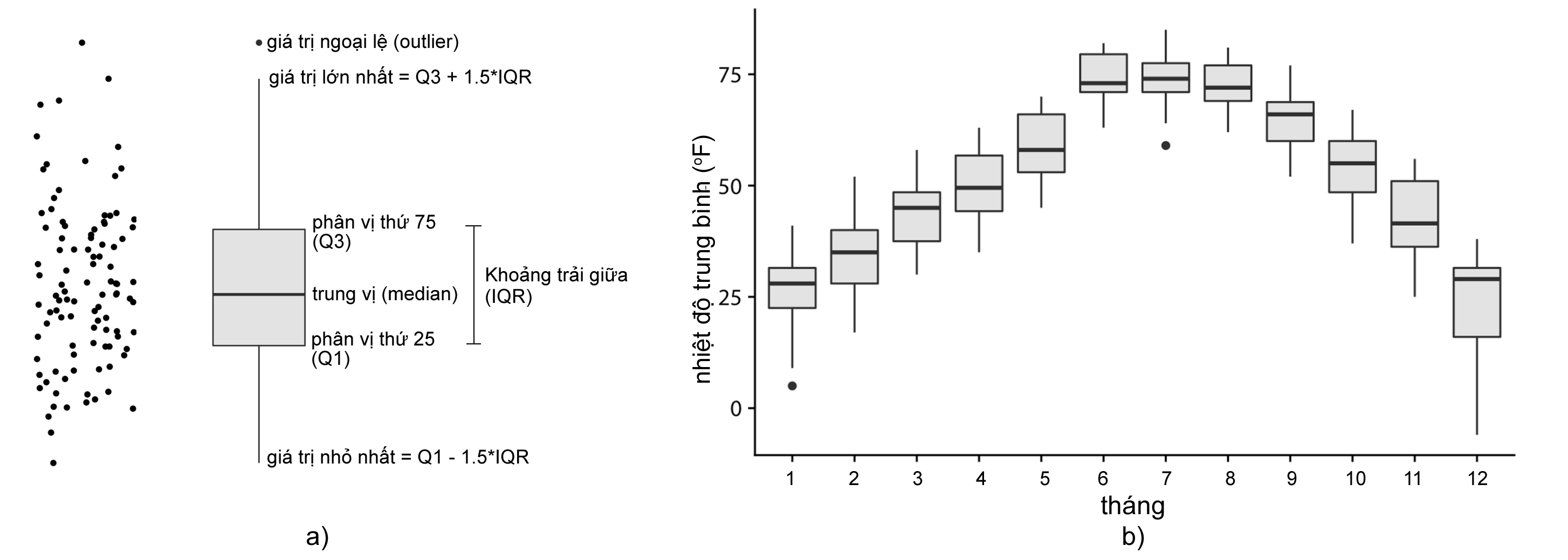
Hình 7. Biểu đồ hộp và trực quan dữ liệu mẫu về nhiệt độ trung bình 12 tháng bằng biểu đồ hộp
(Nguồn: Fundamentals of Data Visualization)
Trong Hình 7b, các biểu đồ hộp được vẽ cạnh nhau để trực quan nhiều phân phối cùng một lúc. Có thể thấy, biểu đồ hộp tuy đơn giản nhưng hiển thị khá rõ ràng về mức chênh lệch nhiệt độ trung bình trong 12 tháng, trong đó nhiệt độ chênh lệch cao vào tháng 12 và ít lệch nhiều trong một số tháng như tháng 7.
Biểu đồ violin (violin plots)
Với khả năng tính toán và trực quan hiện đại, biểu đồ hộp đang dần được thay thế bằng biểu đồ violin. Biểu đồ violin có thể cung cấp một bức tranh dữ liệu chính xác hơn biểu đồ hộp. Biểu đồ violin có tính chất đối xứng, nó bắt đầu và kết thúc ở các giá trị dữ liệu tối thiểu và tối đa, và phần dày nhất của biểu đồ tương ứng với mật độ điểm cao nhất trong tập dữ liệu (Hình 8).
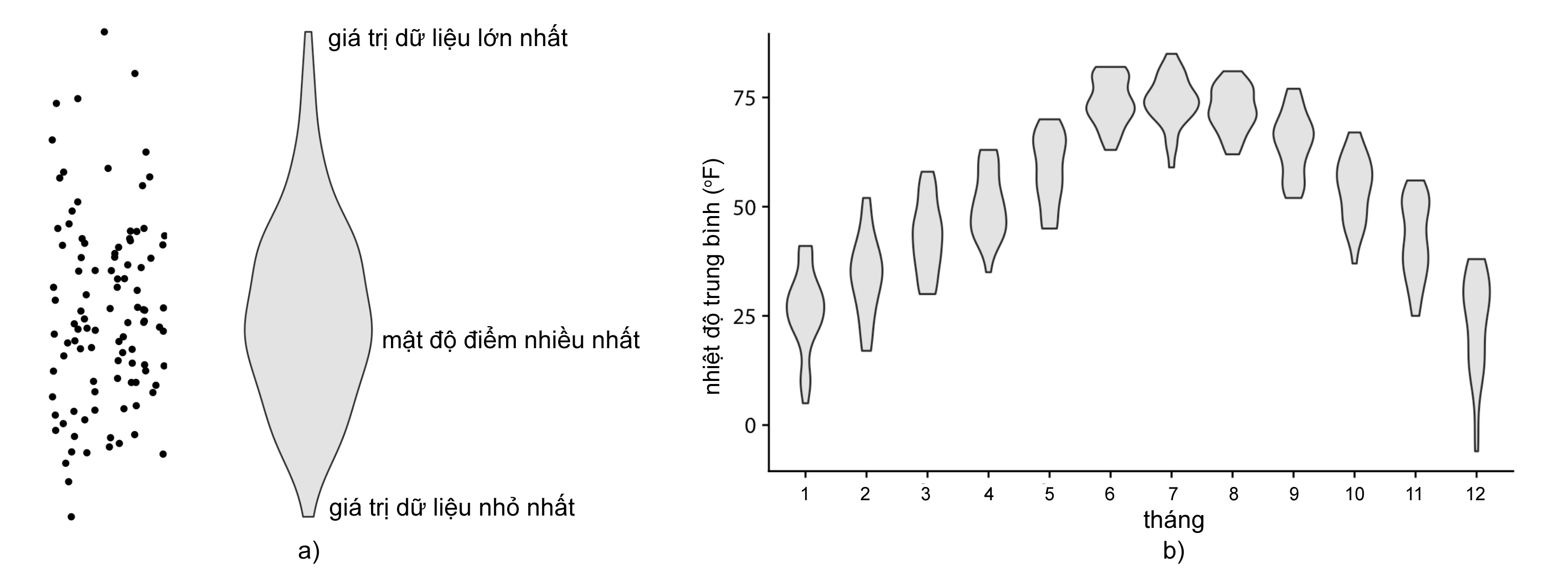
Hình 8. Biểu đồ violin và trực quan dữ liệu mẫu về nhiệt độ trung bình 12 tháng bằng biểu đồ violin
(Nguồn: Fundamentals of Data Visualization)
Do biểu đồ violin được vẽ từ ước tính mật độ nên có thể tạo ra sự xuất hiện của dữ liệu không tồn tại, hoặc thể hiện dữ liệu dày đặc trong khi thực tế khá thưa thớt. Do đó, ta có thể sử dụng biểu đồ sina (sina plots), là sự kết hợp của biểu đồ violin và việc hiển thị tất cả các điểm dữ liệu trên biểu đồ violin để làm nổi bật sự phân bố của dữ liệu (Hình 9).
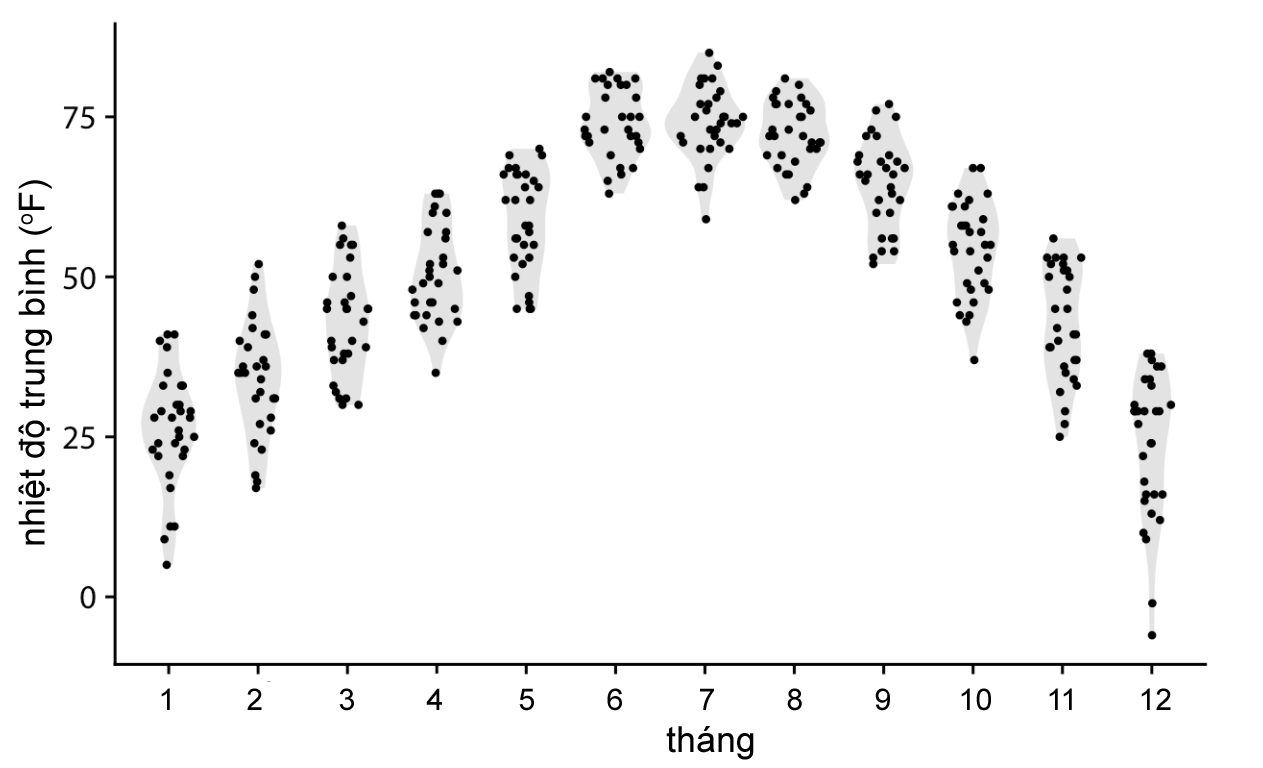
Hình 9. Trực quan dữ liệu mẫu về nhiệt độ trung bình 12 tháng bằng biểu đồ sina
(Nguồn: Fundamentals of Data Visualization)
Biểu đồ ridgeline (ridgeline plots)
Thay vì biểu diễn các phân phối qua các tháng theo trục tung như biểu đồ hộp hay biểu đồ violin, biểu đồ ridgeline sử dụng các biểu đồ mật độ xếp so le với nhau để biểu diễn các phân phối theo hướng thẳng đứng trên trục hoành. Mục đích của biểu đồ ridgeline không phải để hiển thị các giá trị mật độ cụ thể mà là để dễ dàng so sánh các hình dạng mật độ và chiều cao tương đối giữa các nhóm. Các biểu đồ Ridgeline có thể mở rộng quy mô đến số lượng rất lớn các phân bố. Chẳng hạn như trong Hình 10, cho thấy sự phân bố thời lượng phim từ năm 1913 đến năm 2005, có gần 100 sự phân bố khác nhau và nó rất dễ đọc. Có thể thấy, trong những năm 1920, các bộ phim có nhiều thời lượng khác nhau, nhưng từ khoảng năm 1960 đến 2005, thời lượng phim đã được chuẩn hóa thành xấp xỉ 90 phút.
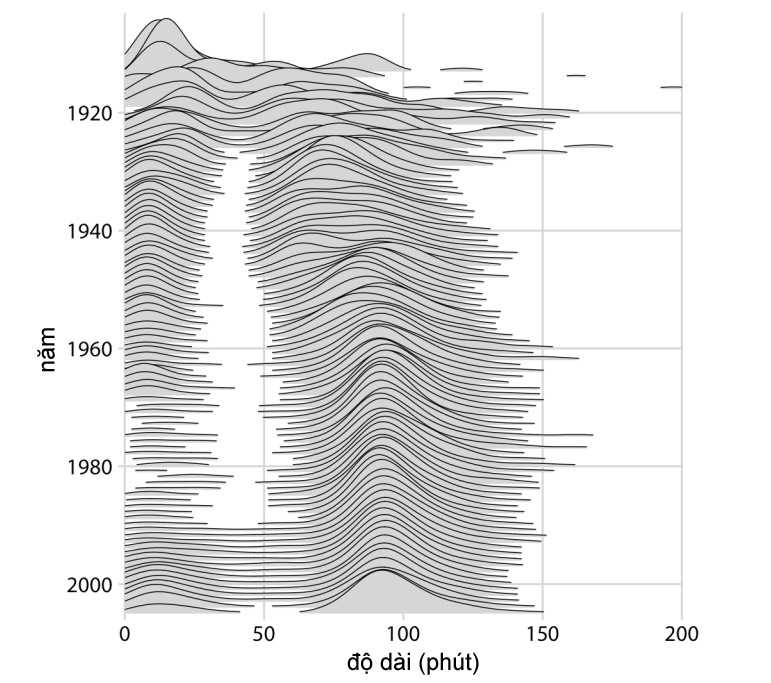
Hình 10. Trực quan dữ liệu mẫu về thời lượng phim từ năm 1913 đến 2005 bằng biểu đồ ridgeline
(Nguồn: Fundamentals of Data Visualization)
Duy Sang tổng hợp
----------------------------------------
Tài liệu tham khảo:
– Wike. (2019). Fundamentals of Data Visualization. Sebastopol: O’Reilly Media.
----------------------------------------
Các bài viết liên quan:
Trực quan hóa dữ liệu – Phần 1: Tổng quan về biểu đồ
Trực quan hóa dữ liệu – Phần 2: Tổng quan về hệ trục tọa độ
Trực quan hóa dữ liệu – Phần 3: Một số dạng biểu đồ thể hiện độ lớn của dữ liệu
Trực quan hóa dữ liệu – Phần 4: Một số dạng biểu đồ thể hiện tỷ lệ của dữ liệu
Trực quan hóa dữ liệu – Phần 6: Các dạng biểu đồ thể hiện sự tương quan của dữ liệu
---------------------------------------------------------------------------------------------------